ラプラス変換LaTeXコード
ラプラス変換 コード置き場
コード置き場
サテライトサイト微分方程式いろいろの新規カテゴリ“ラプラス変換”にて使用された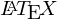 コードになります。
コードになります。
なお近年サテライトサイト「よくわかる慣性モーメント」をはじめとした当Webサイト管理人が運営するサイトのコンテンツ盗用が目立ちます。参考にする場合は紹介のバックリンクを貼るなどといった、社会人としての最低限のルール、マナーを守る対応は必ずお願いします。
ラプラス変換の定義式
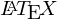 コード
コード
\begin{eqnarray*}
\lim_{M\;\rightarrow\;\infty}\int^{M}_{0}f\left(\:t\:\right)\:e^{-st}dt\:=\:\int^{\infty}_{0}f\left(\:t\:\right)\:e^{-st}dt
\end{eqnarray*}
出力画像
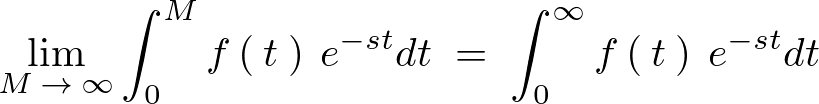
ポイントは上記の極限の![]() はlimの前に\をつけて極限のlimitであることを指示させてそのあとにアンダーバーの_をつけて{}をつけます。その{}の中に極限操作の
はlimの前に\をつけて極限のlimitであることを指示させてそのあとにアンダーバーの_をつけて{}をつけます。その{}の中に極限操作の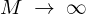 のコードを入れます。
のコードを入れます。
 コード
コード
\begin{eqnarray*}
\mathcal{\:L\:}\left[\:1\:\right]\;&=&\;\int^{\infty}_{0}1\cdot e^{-st}dt\nonumber\\
&=&\;\int^{\infty}_{0}\cdot e^{-st}dt\nonumber\\
&=&\;\left[\:-\frac{1}{s}e^{-st}\:\right]^{\infty}_{0}\nonumber\\
&=&\;-\frac{1}{s}\left(\:e^{-\infty}\;-\;e^{-0}\:\right)\nonumber\\
&=&\;\frac{1}{s}\nonumber\\
\end{eqnarray*}
出力画像
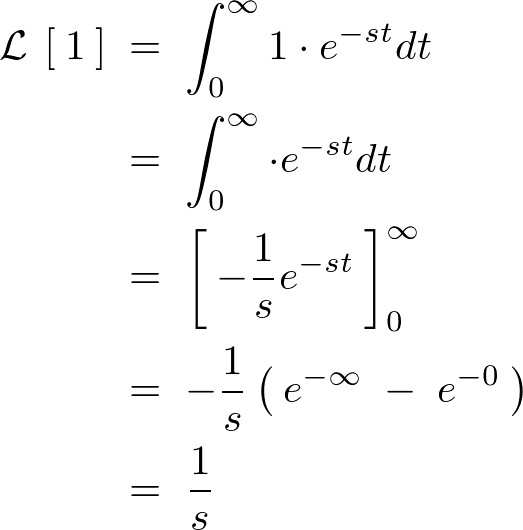
定数以外のラプラス変換
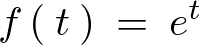 の場合のラプラス変換
の場合のラプラス変換
 コード
コード
\begin{eqnarray*}
\int^{\infty}_{0}e^{-st}\cdot e^{t}dt\;&=&\;\int^{\infty}_{0}e^{-\left(\:s\:-\:1\:\right)t}dt\\
&=&\int^{\infty}_{0}e^{-\omega}\:\frac{d\omega}{1\:-\:s}\\
&=&\frac{1}{1\:-\:s}\int^{\infty}_{0}\:e^{-\omega}\:d\omega\\
&=&\frac{1}{1\:-\:s}\Big[\:-e^{-\omega}\:\Big]^{\infty}_{0}\\
&=&\frac{1}{1\:-\:s}\Big\{\:e^{-\infty}\;-\;\left(\:-e^{-0}\:\right)\:\Big\}\\
&=&\frac{1}{1\:-\:s}\left(\:0\;+\;1\:\right)\\
&=&\frac{1}{1\:-\:s}\\
\end{eqnarray*}
出力画像
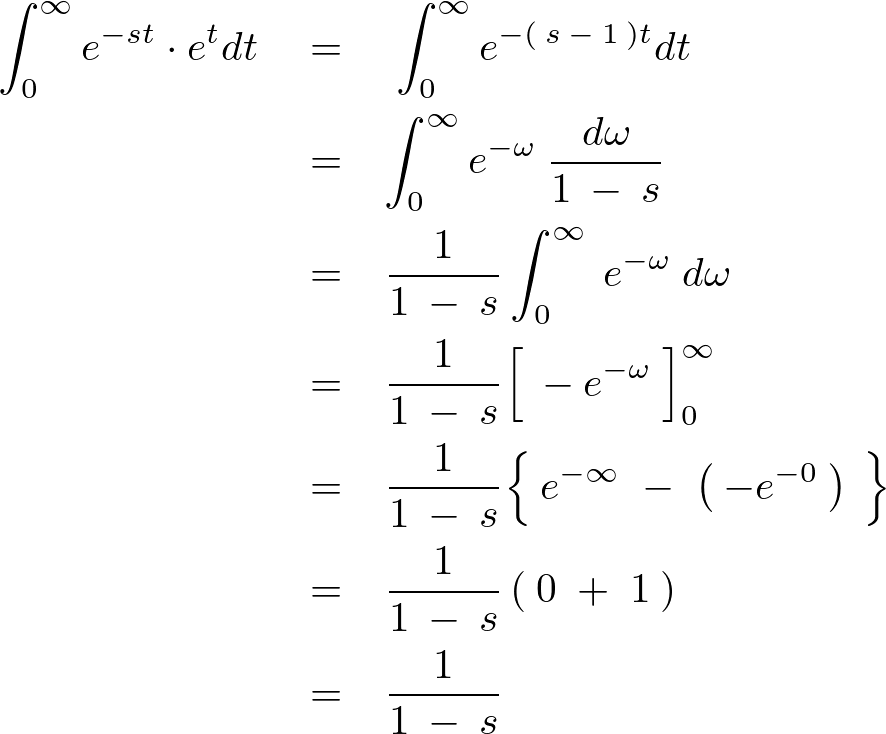
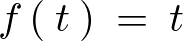 の場合のラプラス変換
の場合のラプラス変換
 コード
コード
\[
F\left(\:s\:\right)\;=\;\mathcal{\:L\:}\left[\:f\left(\:t\:\right)\:\right]\;=\;\mathcal{\:L\:}\left[\:t\:\right]
\]
\begin{eqnarray*}
F\left(\:s\:\right)&=&\int^{\infty}_{0}t\cdot e^{-st}\:dt\\
&=&\left[\:t\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)\:\right]^{\infty}_{0}\:-\:\int^{\infty}_{0}\frac{dt}{dt}\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)dt\\
&=&\qquad 0\qquad +\qquad\frac{1}{s}\int^{\infty}_{0}e^{-st}\:dt\\
\mathcal{L}\left[\:t\:\right]&=&\frac{1}{s}\int^{\infty}_{0}e^{-st}\:dt\\
&=&\frac{1}{s}\left[\:-\frac{1}{s}e^{-st}\:\right]^{\infty}_{0}\\
&=&-\frac{1}{s^2}\left(\:e^{-\infty}\;-\;e^{0}\:\right)\\
&=&\frac{1}{s^2}
\end{eqnarray*}
\begin{eqnarray*}
\mathcal{L}\left[\:t\:\right]&=&\frac{1}{s}\int^{\infty}_{0}e^{-st}\:dt\\
\mathcal{L}\left[\:t\:\right]&=&\frac{1}{s}\int^{\infty}_{0}e^{-st}\:dt\\
&=&\frac{1}{s}\left[\:-\frac{1}{s}e^{-st}\:\right]^{\infty}_{0}\\
&=&-\frac{1}{s^2}\left(\:e^{-\infty}\;-\;e^{0}\:\right)\\
&=&\frac{1}{s^2}
\end{eqnarray*}
出力画像
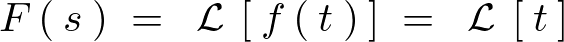
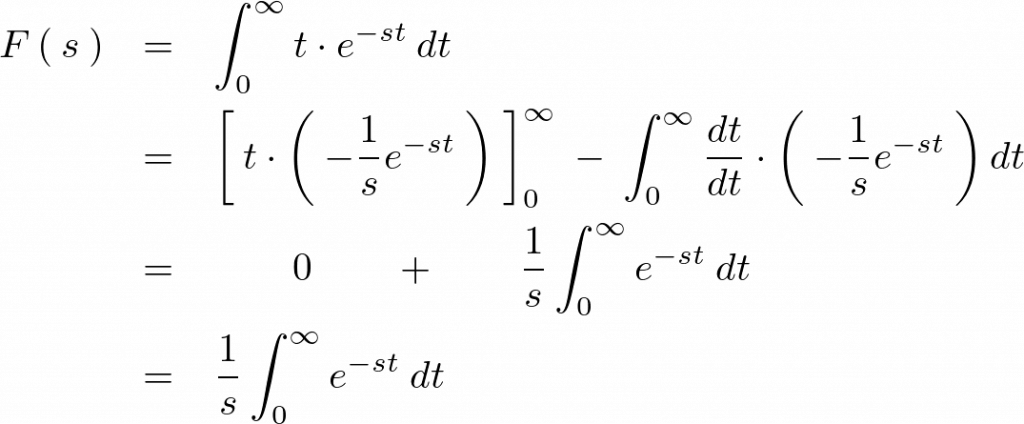
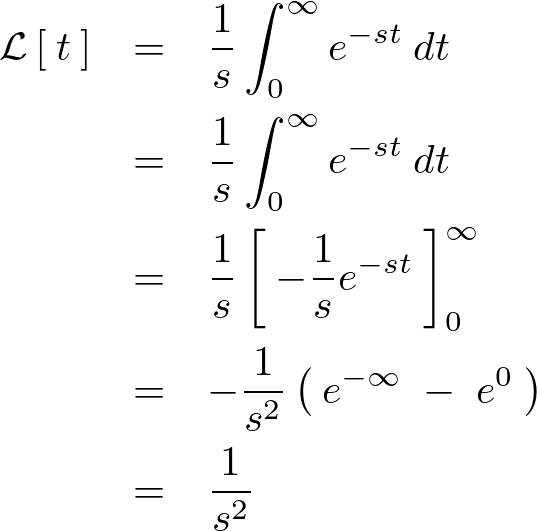
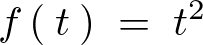 の場合のラプラス変換
の場合のラプラス変換
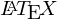 コード
コード
\begin{eqnarray*}
\mathcal{\:L\:}\left[\:t^2\:\right]&=&\int^{\infty}_{0}t^2\cdot e^{-st}dt\\
&=&\left[\:t^2\left(\:-\frac{1}{s}e^{-st}\:\right)\:\right]^{\infty}_{0}-\int^{\infty}_{0}\frac{d\:t^2}{dt}\cdot\left(\:-\frac{1}{s}e^{-st}\:\right)dt\\
&=&0\;+\;\frac{1}{\;s\;}\int^{\infty}_{0}2t\cdot e^{-st}dt\\
&=&\frac{2}{\;s\;}\int^{\infty}_{0}t\cdot e^{-st}dt\\
&=&\frac{2}{\;s\;}\left\{\;\left[\:t\cdot\left(\:-\frac{1}{\;s\;}e^{-st}\:\right)\:\right]^{\infty}_{0}\;-\;\int^{\infty}_{0}\frac{d}{dt}t\cdot\left(\:-\frac{1}{\;s\;}e^{-st}\:\right)dt\;\right\}\\
&=&\frac{2}{\;s\;}\left(\:\quad 0\quad \;+\;\frac{1}{\;s\;}\int^{\infty}_{0}e^{-st}dt\:\right)\\
&=&\frac{2}{\;s^2\:}\int^{\infty}_{0}e^{-st}dt\\
&=&\frac{2}{\;s^2\:}\left[\:-\frac{1}{\;s\;}e^{-st}\:\right]^{\infty}_{0}\\
&=&-\frac{2}{\:s^3\:}\Big[\:e^{-\infty}\;-\;e^0\:\Big]\\
&=&\frac{2}{\:s^3\:}\\
\end{eqnarray*}
出力画像
-
diff-eq.comスケールアップマイグレーション4
カテゴリー
-
diff-eq.comスケールアップマイグレーション3
-
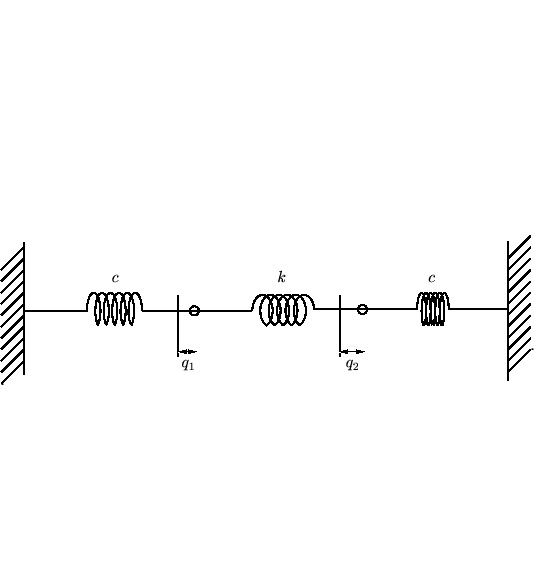
連成振動の解②━LaTeXコード置き場
カテゴリー
-
diff-eq.comスケールアップマイグレーション2
-

diff-eq.comスケールアップマイグレーション1
-

サブネットマスクの計算
カテゴリー