年金終価係数
複利計算による将来の価格(終価という考え)
一般的にただ漠然と利潤のみを狙って投資をしているなら別ですが将来いったいいつまでに、かつ毎月いくら積み立てていきたいと考えるような堅実な運用である場合、大体の期間を定めて年間何%の金利を設定すれば将来いったいいくらになるかという計算を行う場合がおおいかと思います。
仮に年利率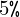 で運用していった場合、一年後には元本
で運用していった場合、一年後には元本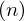 も含めた金額は
も含めた金額は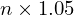 になるものだというものであって、例えば100万円を一年間運用すれば105万となります。
になるものだというものであって、例えば100万円を一年間運用すれば105万となります。
そしてその金利には単利と複利があります。
ここでひとまず元本を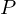 、年間利率を
、年間利率を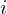 、終価としての変数を
、終価としての変数を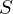 、さらに利息を
、さらに利息を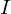 、投資期間を
、投資期間を![]() 年間と置いた場合、その期間内における単利による利息
年間と置いた場合、その期間内における単利による利息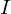 は、
は、
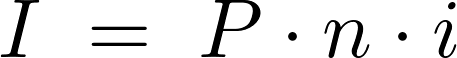
なので元利合計は次のようになります。
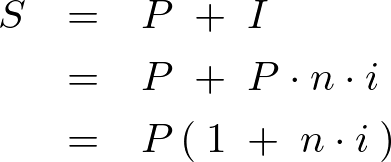
この出てきた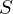 を先ほども言った終価という呼び方をします。
を先ほども言った終価という呼び方をします。
複利計算
複利計算においては一年を経過した元利合計をさらに次の年度の投資元金に組み入れるというものなので、
1年後の元利合計

2年後の元利合計
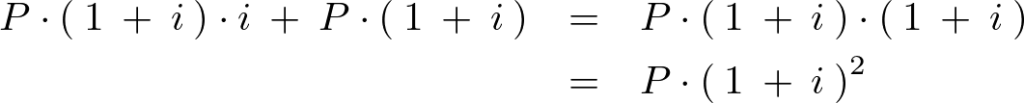
結果的にこれの繰り返しになるので![]() 年後の複利計算における元利合計
年後の複利計算における元利合計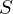 (終価)は、
(終価)は、
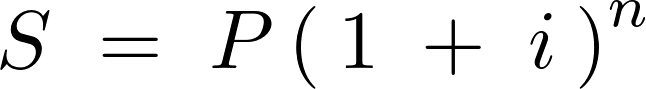
この上記式を変形させると次のような表現ができます。
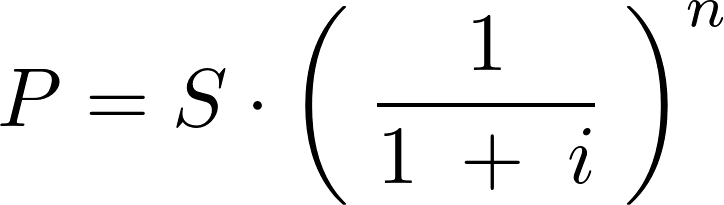
通常の場合だと最初に元本を確保して、それを運用して将来の価格(終価)を予想するものですが、この式を利用すると例えば十数年後に○○○○万円を目標に利殖していった場合、最初に用意する元本はいくら必要になるか?という計算が可能になることがわかります。
仮に年利3%、20年間運用できたとし、終価5000万円を得たいのであれば以下のような計算になります。
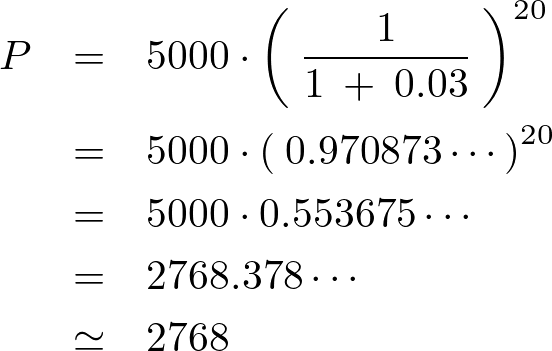
約2768万円の元本を用意するという結果が出ます。
期始払い確定年金終価
上記の式をさらに発展させた式で期始払い確定年金終価という数式があります。
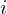 を年利率、
を年利率、![]() を年数として次のように表します。
を年数として次のように表します。


![]() の上にツードットがありますがこれはニュートン表記の2階微分記号によるものではなく生命保険数学分野において使われる専用の表記になります。
の上にツードットがありますがこれはニュートン表記の2階微分記号によるものではなく生命保険数学分野において使われる専用の表記になります。
参考までに追記すると次のようなものもあります。
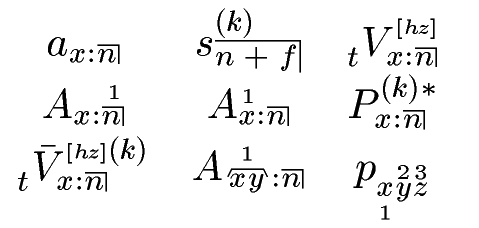
期始払い年金終価係数
ex.年利5%での20年間運用で5000万
仮に年利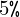 で20年間運用できたとし、その20年後に5000万円を目標にしたとします。そうした場合の毎年始めに用意する金額がいくらになるかを実際に期始払い年金終価の式に代入して導き出してみましょう。
で20年間運用できたとし、その20年後に5000万円を目標にしたとします。そうした場合の毎年始めに用意する金額がいくらになるかを実際に期始払い年金終価の式に代入して導き出してみましょう。
年利: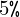 、年数:20年
、年数:20年

毎年始めに用意する金額を“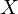 ”と置くと、終価5000万なので次のような恒等式が成り立ち求める金額
”と置くと、終価5000万なので次のような恒等式が成り立ち求める金額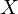 が決まります。
が決まります。

毎年初めに用意する金額が約144万円ほど。これを毎年複利で運用していった場合20年後には目標の金額に達成することができます。
ただし毎年同じ金利で運用できた場合であり、経済環境は常日頃変化しているので運用金利が変更になった場合は途中で工夫する必要があります。
実際の個人投資家としての運用環境を考慮

基本的に年の始めにその後に運用する金額をボンっと用意するとしていますが、もともと蓄えがある人は別として実際にはそうそう簡単にこれだけの金額をいきなり用意するのは難しいし、またたとえそれを用意するだけの蓄えがあったとしても、一般的な社会生活をしている人であれば、毎月の給与から生活費などのコストを除いた可処分所得を毎月貯蓄に回している場合がほとんどかと思います。
要するに蓄えがある余裕ある人でも野球選手のような年棒制でもない限り、投資などに回せる金額が毎月ごとに発生しているはずです。
なので期始払い年金終価における年利率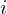 を次のようにしてみます。
を次のようにしてみます。

月ごとにある一定の金額を運用投資に回して決められたある時期に決められたある金額をためるには、毎月いったいいくらの金額を用意すればよいか、その金額を表示させるエクセルシートを実際に作ってみました。
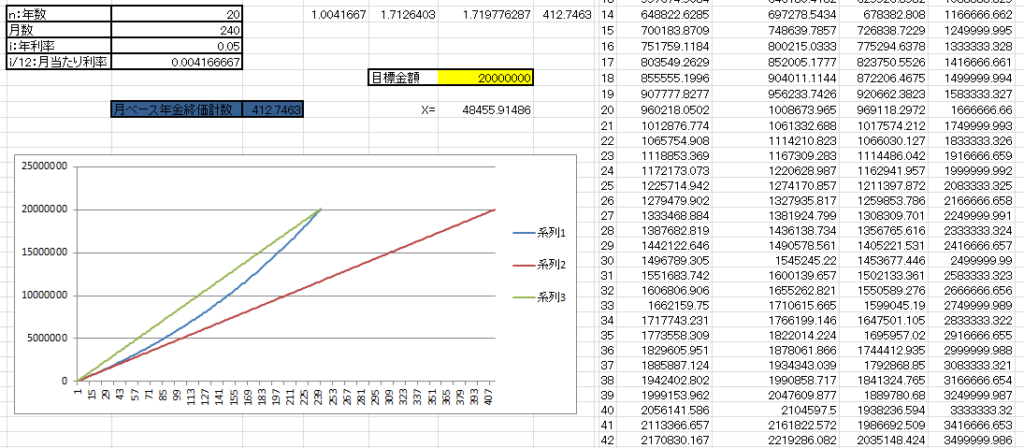

上記画像では年利5%で運用していき、20年後(240か月後)に2000万円をためるには毎月いったいいくら投資に回せばよいかその結果が表示されています。下側の計算式が月ごとの年金終価係数になり、仮に毎年年利5%で運用できた場合、月額あたり4万8千円ほど運用投資に回せばいいという結果になります。

このグラフを見てわかるように、運用投資をするのとしないのとでは20年後の金額の差に大きな開きができ、単に同一金額を貯蓄に回した場合との金額の差は歴然で、アインシュタインが人類の最大の発明が“複利だ”といったのが何となく理解できます。
ただし上記の例のような毎年年利5%で運用し続けることはプロでもなかなか難しく、一般の方ではなおさらのことらしいです。
外部リンク:分散投資で年利3%の運用を目指す
https://www.nikkei.com/article/DGXNMSFK1102C_R10C12A7000000
上記のリンク先の内容だと5%での運用は難しくとも3%での運用ならばある程度は目指せるらしいとのこと。
仮に目標額を2~3000万ほどとし、それを30年ぐらい続けるとした場合は3~5万円程度の毎月の積立になりますが負担なく毎月続けるにはこれぐらいの金額が現実的なのだそうです。
実際に手元にある年金終価係数エクセルシートを使って年利率3%で30年間運用の目標額3000万円とした場合、毎月の積立額を計算すると約5万円という金額になります。
運用しない場合と比べると毎月3万円強の違いが出てきますが、毎月のこととなるとやはり少ない金額とは言えません。
これらはとりわけ小難しい数学の知識は使っていませんのでグラフ表示ができるような係数算出の簡単なエクセルシートなどをご自分で作ってみるのも面白いかと思います。
-
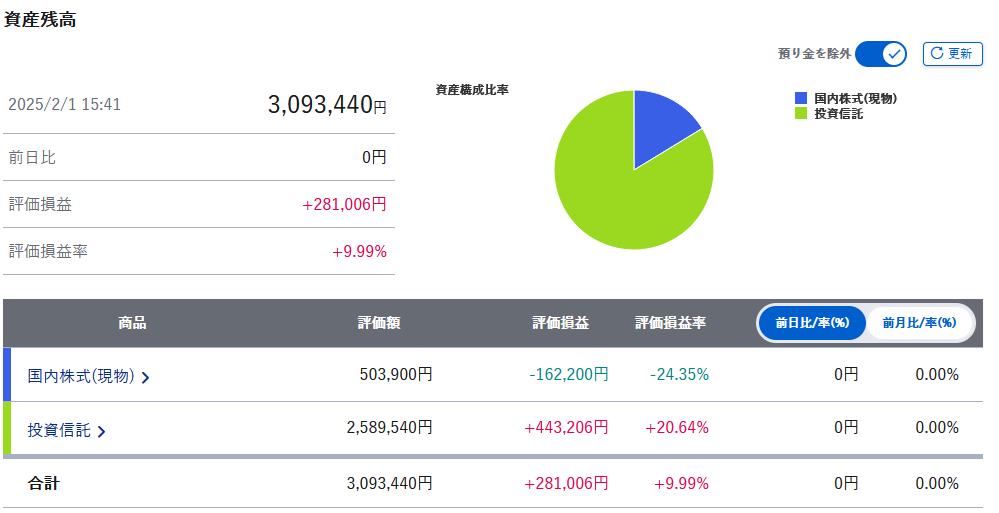
2025年1月NISA運用概況
カテゴリー
-

2025年1月金運用概況
カテゴリー
-
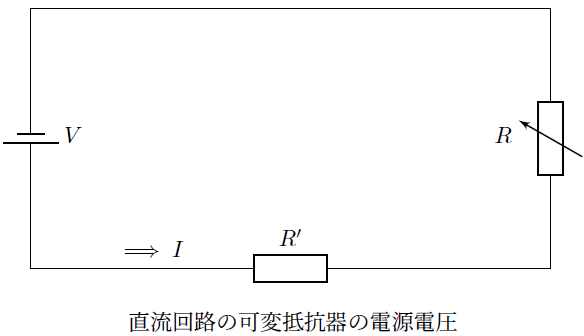
可変抵抗器の直列回路
カテゴリー
-
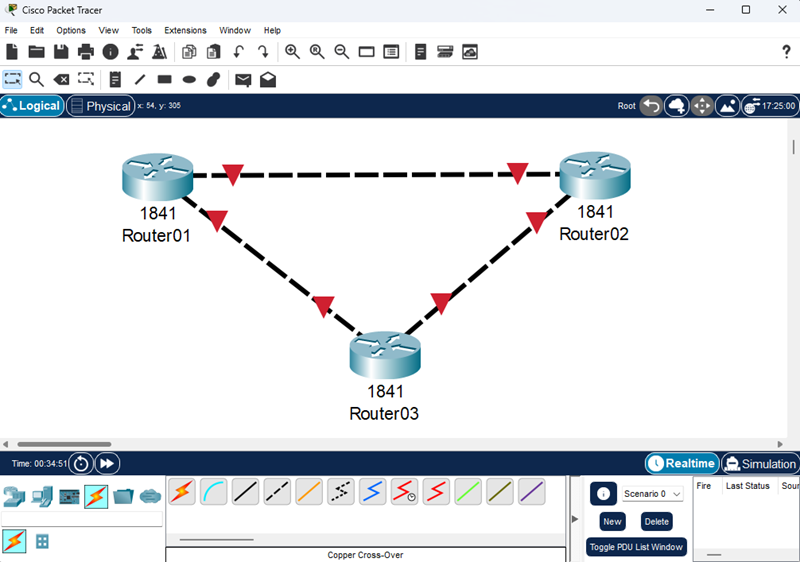
Packet Tracer
カテゴリー
-
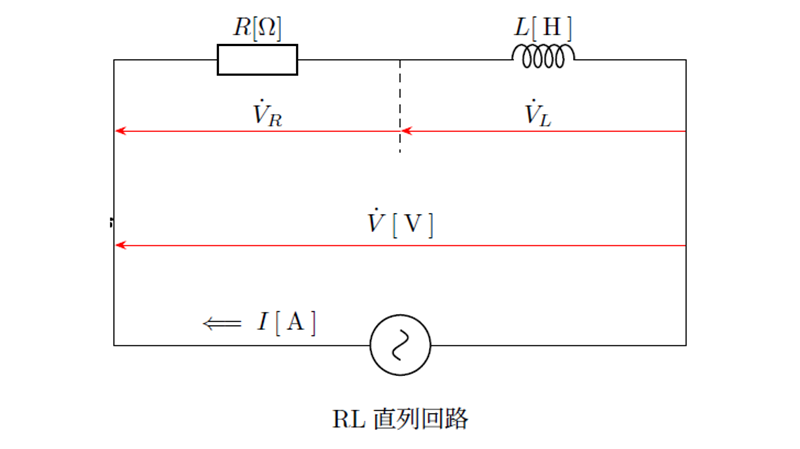
交流回路の直列接続
カテゴリー
-
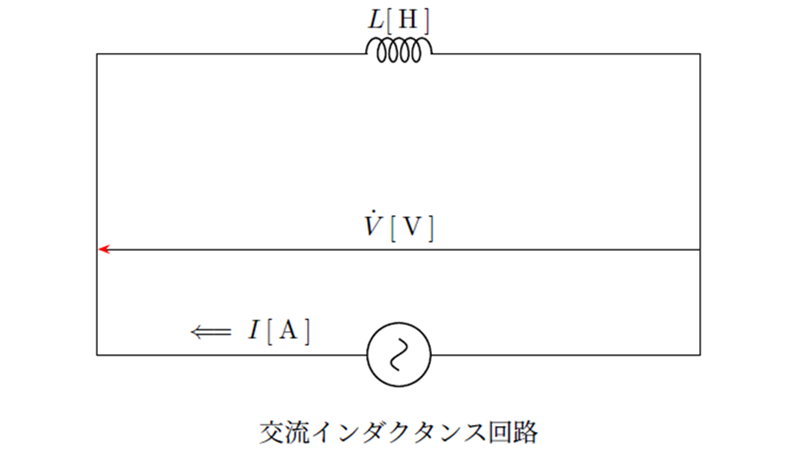
交流回路
カテゴリー
テスト投稿
-

2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-

可変抵抗器の直列回路
続きを読む
-

Packet Tracer
続きを読む
-

交流回路の直列接続
続きを読む
-

交流回路
続きを読む