ラプラス方程式
サテライトサイト「微分方程式いろいろ」コンテンツ内で取り上げた「ラプラス方程式」にて使用されたPythonグラフィックスになります。
ラプラス方程式とは、2階の線型楕円型偏微分方程式のことになります。領域内においてある境界条件を満たすラプラス方程式を求め、それによりさまざまな解析解を導くことが可能です。
ここでは簡単な例として長方形プレートの平衡温度分布に関して、2次元のラプラス方程式で導き出した解をPythonの3次元描画によって表現します。
ラプラス演算子
ひとまずラプラス方程式に関しての簡単な予備知識を考察していきます。
それぞれの座標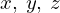 とした3次元座標空間において2階の偏微分作用素を
とした3次元座標空間において2階の偏微分作用素を とし、この作用素を次のようにおきます。
とし、この作用素を次のようにおきます。

ここでナブラと呼ばれる次のもの、
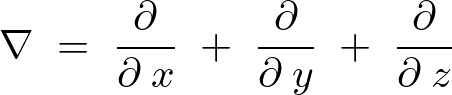
これを使って表せば上記式の2階偏微分作用素式の右辺は次のようなものになります。
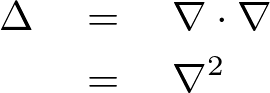
ラプラス方程式とは、考えうるそれぞれの次元において付与される作用素の2階微分に関して、そのラプラス作用素を用いて表現すると次のようなものになります。
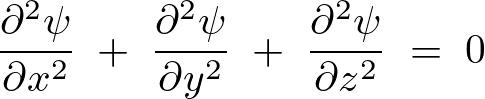
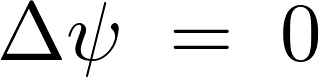
上記式をみてわかるようにラプラス方程式には時間に当たる変数![]() が含まれていません。それにより時間によって変化しない定常状態を表します。時間を反映した変数がないため、このために初期条件はなく、次に示すような境界条件だけが必要となります。
が含まれていません。それにより時間によって変化しない定常状態を表します。時間を反映した変数がないため、このために初期条件はなく、次に示すような境界条件だけが必要となります。
ディリクレ境界条件
ここでは長方形プレートとみなした場合の以下のようなもの、
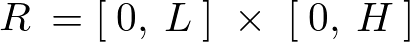
とした、2次元でのラプラス方程式の考察をしていきます。
境界条件として次のようなものとします。

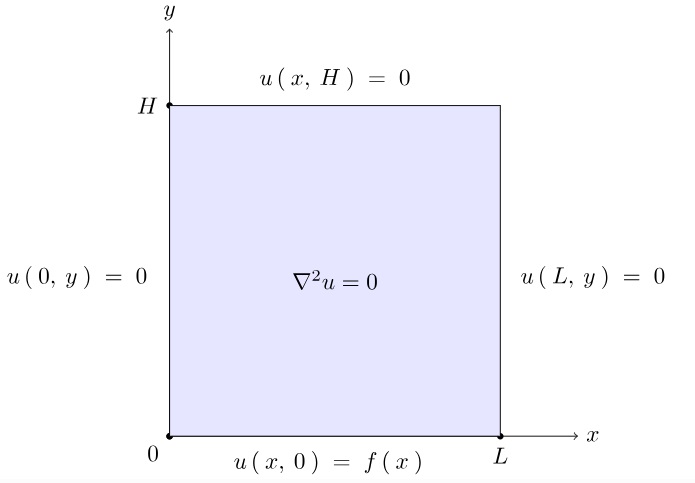
図示すると次のようなものになります。
このような境界条件から変数分離法などを使って最終的に求まる解が以下のようになります。

ただし上記式の![]() に関しては以下のようになります。
に関しては以下のようになります。

これの導出に関してはこちらを参照ください。
Pythonコード
インポートするのは以下になります。
import numpy from matplotlib import pyplot from matplotlib import rcParams from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm
次にfigureインスタンスを作成して、add_subplot()メソッドで3D用の軸を追加します。add_subplot()メソッドの第1引数の「111」は、行、列、インデックスを表しています。次にように追記します。
def plot_3D(x, y, p):
fig = pyplot.figure(figsize=(20,10), dpi=80)
ax = fig.add_subplot(111, projection='3d')
X,Y = numpy.meshgrid(x,y)
surf = ax.plot_surface(X,Y,p[:], rstride=1, cstride=1, cmap=cm.gist_heat, linewidth=0, antialiased=False)
matplotlibでグラフの描画範囲の設定
次のようにして範囲指定をします。
ax.set_xlim(0,1)
ax.set_ylim(0,1)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_zlabel('$z$')
ax.view_init(20,40)
def構文で関数の定義
defで関数p_analyticalを定義しmeshgridで要素列を作成します。処理関数の部分に上記求められたラプラス方程式(sinh)の処理構文を入力します。
def 関数名(引数1, 引数2, ...):
処理関数式(ラプラス方程式)
return 戻り値
def p_analytical(x, y):
X, Y = numpy.meshgrid(x,y)
p_an = numpy.sinh(1.0*numpy.pi*Y / x[-1]) /\
(numpy.sinh(1.0*numpy.pi*y[-1]/x[-1]))*numpy.sin(1.0*numpy.pi*X/x[-1])
return p_an
全体としては以下のような記述になります。
from matplotlib import pyplot
import numpy
from matplotlib import rcParams
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
def plot_3D(x, y, p):
fig = pyplot.figure(figsize=(20,10), dpi=80)
ax = fig.add_subplot(111, projection='3d')
X,Y = numpy.meshgrid(x,y)
surf = ax.plot_surface(X,Y,p[:], rstride=1, cstride=1, cmap=cm.gist_heat, linewidth=0, antialiased=False)
ax.set_xlim(0,1)
ax.set_ylim(0,1)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_zlabel('$z$')
ax.view_init(20,40)
def p_analytical(x, y):
X, Y = numpy.meshgrid(x,y)
p_an = numpy.sinh(1.0*numpy.pi*Y / x[-1]) /\
(numpy.sinh(1.0*numpy.pi*y[-1]/x[-1]))*numpy.sin(1.0*numpy.pi*X/x[-1])
return p_an
nx = 40
ny = 40
x = numpy.linspace(0,1,nx)
y = numpy.linspace(0,1,ny)
p_an = p_analytical(x,y)
plot_3D(x,y,p_an)
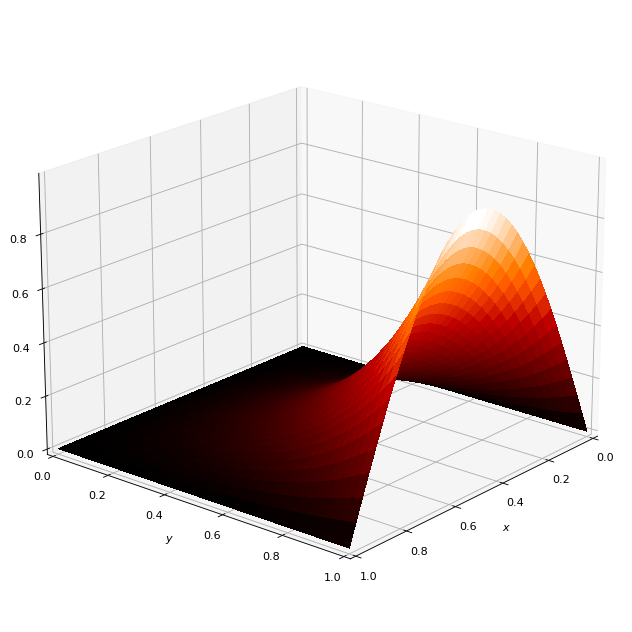
これを実行させることによって以下のようなディリクレ条件を満たすラプラス方程式の描画が出力されます。
-
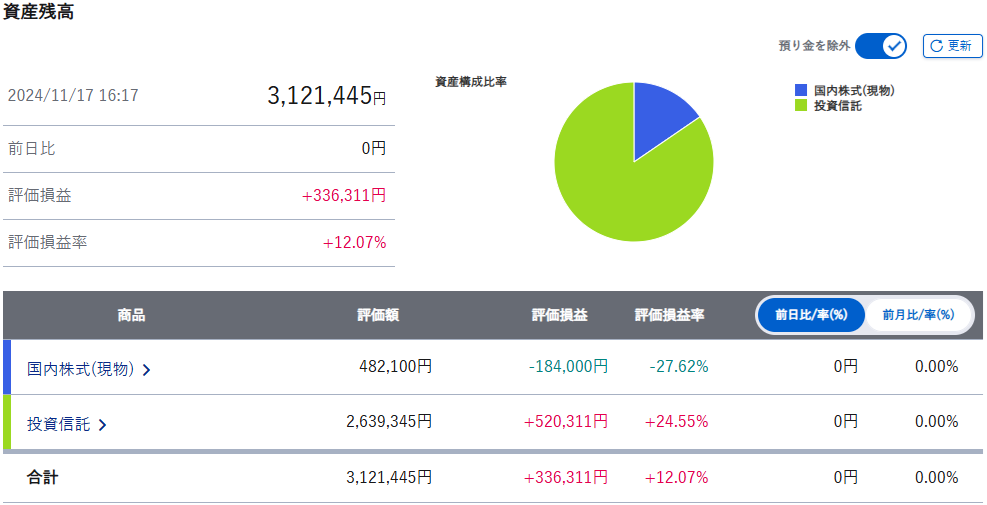
2024年NISA運用概況
続きを読む
-
NISA運用概況
続きを読む
-
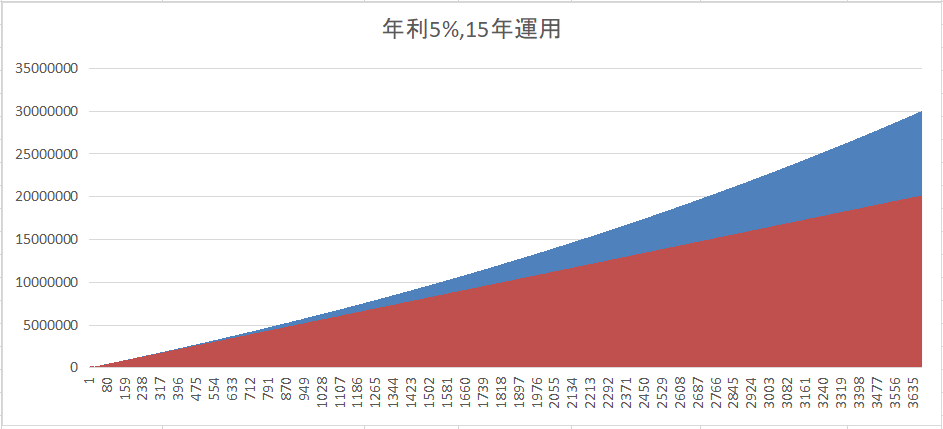
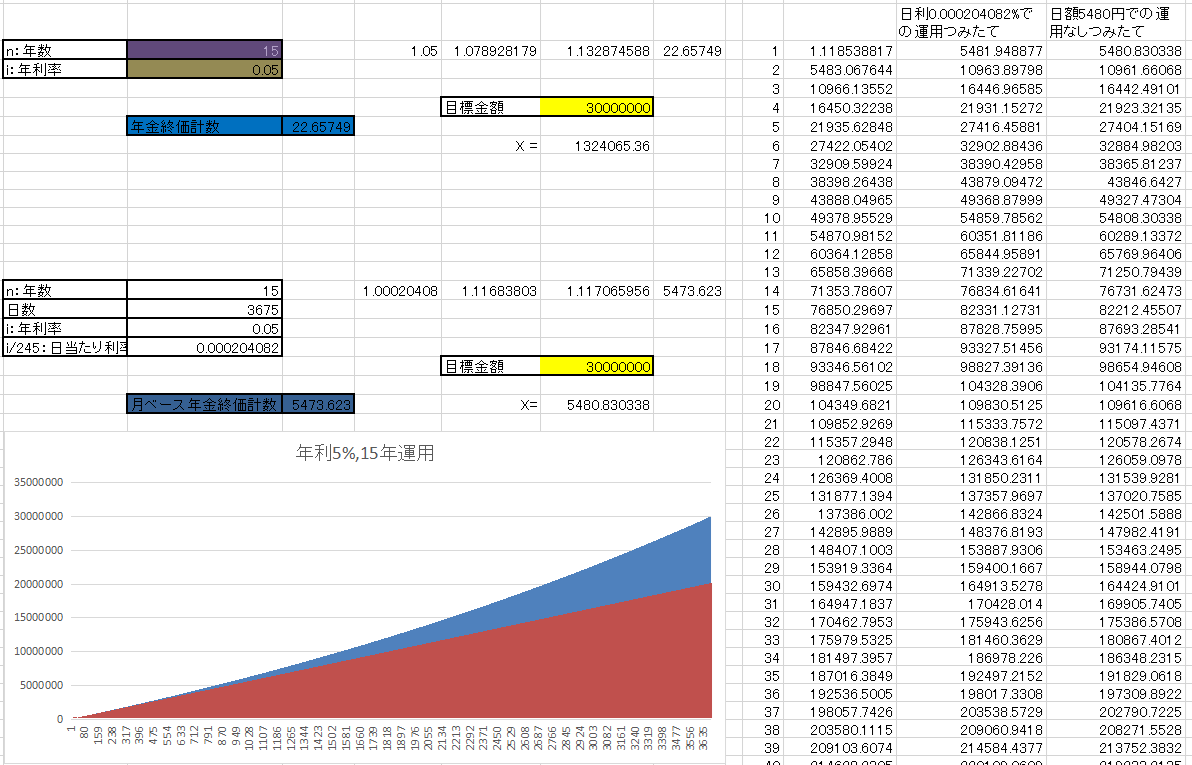
アッパーマス層と年金終価係数
続きを読む
-
重複分散適宜売却型日別ドルコスト平均法
続きを読む
-
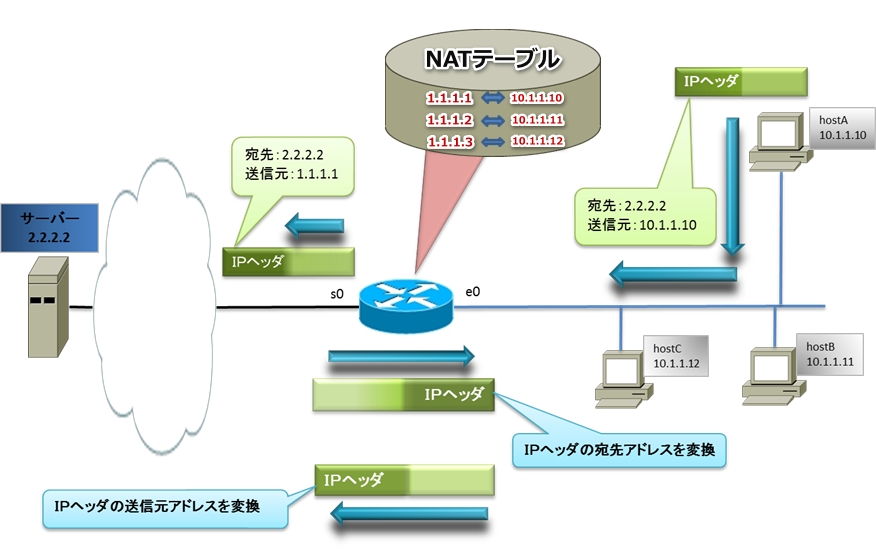
ネットワーキングラボ
続きを読む
-
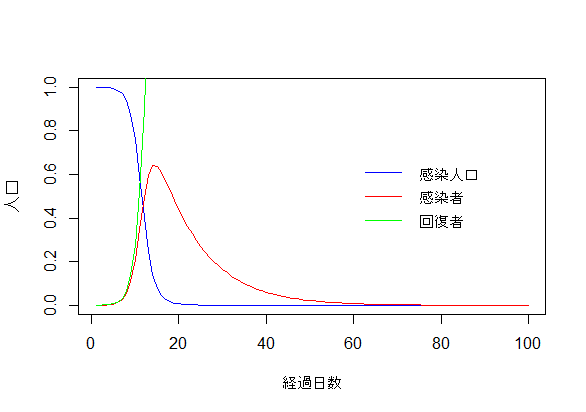
RstudioでSIRモデル②
続きを読む
テスト投稿
-

2024年NISA運用概況
続きを読む
-

NISA運用概況
続きを読む
-

アッパーマス層と年金終価係数
続きを読む
-

重複分散適宜売却型日別ドルコスト平均法
続きを読む
-

ネットワーキングラボ
続きを読む
-

RstudioでSIRモデル②
続きを読む