AnacondaによるPython数学とその描画

Anaconda　Promptの起動

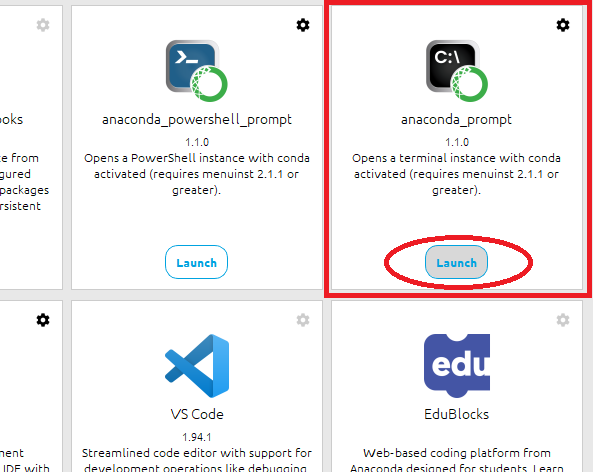
前回インストールしたAnacondaを立ち上げたらキャプチャ画像の赤囲み部分のanaconda_promptのLaunchをクリックしてprompt画面を開きます。

コマンドプロンプトが開いたら次のように打ち込んで対話型Pythonの実行環境であるPython Promptを起動させます。

(c) Microsoft Corporation. All rights reserved.

(base) C:\Users\user>python

上記のようにPythonと打ち込んでEnterを押下し以下のようなメッセージ、>>>という入力モードになっていれば問題なく実行環境が反映されます。

(c) Microsoft Corporation. All rights reserved.

(base) C:\Users\user>python
Python 3.12.7 | packaged by Anaconda, Inc. | (main, Oct  4 2024, 13:17:27) [MSC v.1929 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>>

関数の描画

三角関数

まずは三角関数の描画から行います。

の描画

C:\WINDOWS\system32>python
Python 3.6.0 |Anaconda 4.3.0 (64-bit)| (default, Dec 23 2016, 11:57:41) [MSC v.1900 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 16, 0.001)
y = np.cos(x)
plt.plot(x,y)

plt.show()

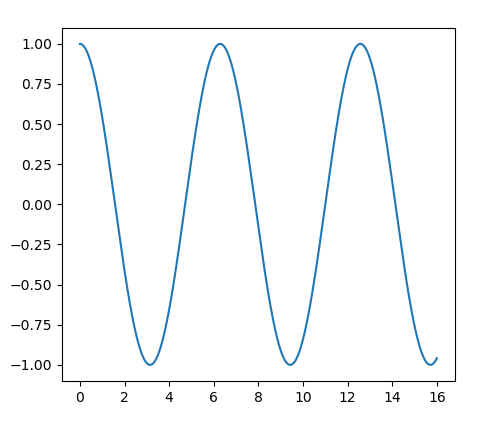
importをし、xの幅を範囲指定します。
コサインならcos(x)と入力して上記のようにコードを入力、または上記のコード（import numpy as npから下の部分）をコピペしてそのまま張り付けてEnterキーを押せば左のような画像が簡単に出力されます。

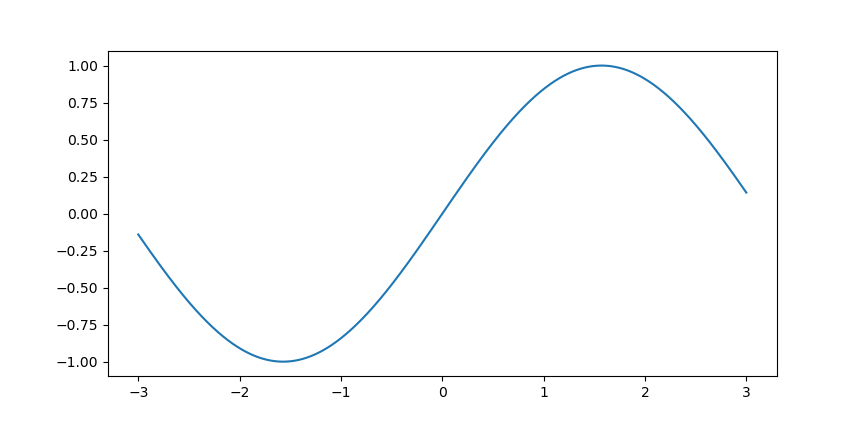
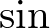の描画

先ほどと同じようにしてcosの部分のみをsinに変えます。ｘの値幅は自分で好きなように変えるとよいでしょう。

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-3, 3, 0.001)
y = np.sin(x)
plt.plot(x, y)

plt.show()

正規分布関数

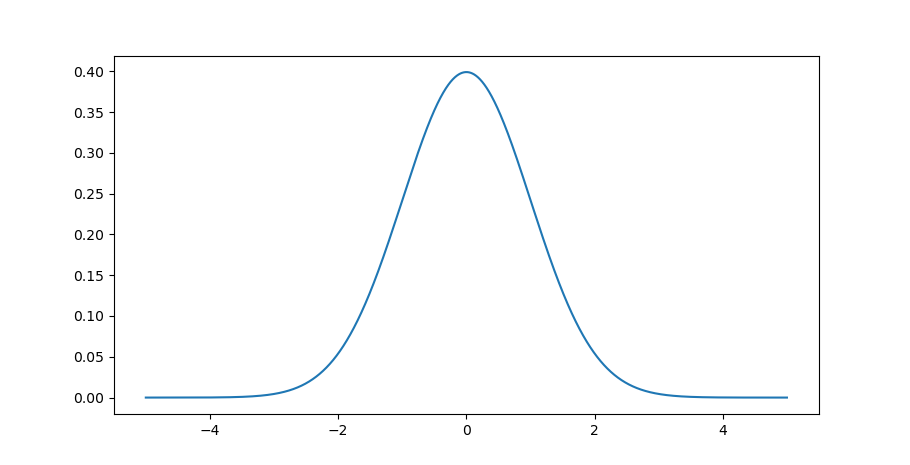
上の図のような釣り鐘型のグラフを一般的に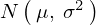で表しその内容を具体的な数式で表記すると次のようなものになります。

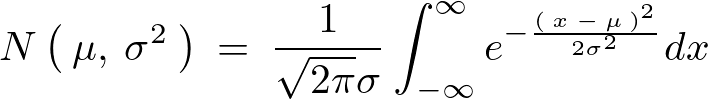
上記式中の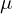は平均、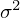は分散を意味しています。

次のようにして入力します。

import numpy as np
from matplotlib import pyplot as plt
sigma = (1.0)
mu = (0)
x = np.arange(-5, 5, 0.001)
y = (1/np.sqrt(2 * np.pi * sigma)) * np.exp(-(x - mu)**2 / 2 * sigma**2)
plt.plot(x, y)

plt.show()

正規分布関数の定積分計算

標準正規分布関数をプラス側とマイナス側に分けて実際に定積分し、同じ値が出るか確認してみましょう。
簡単のために平均のミューは０、分散は１として計算します。

次のように入力していきます。

from sympy import Symbol, exp, sqrt, pi, Integral
x = Symbol('x')
y = exp(-(x)**2/2)/sqrt(2*pi)
Integral(y, (x, 0, 1)).evalf()
0.341344746068543

0.341344746068543という値が出ました。
次にｘの定積分範囲を-1から0に指定してその値を出力します。

Integral(y, (x, -1, 0)).evalf()
0.341344746068543

同じ0.341344746068543という値になります。
また積分範囲を-1から1のように指定すると、

Integral(y, (x, -1, 1)).evalf()
0.682689492137086

と出るので２倍した数値が出てきます。

一連の流れを示すと次のようになります。

>>> from sympy import Symbol, exp, sqrt, pi, Integral
>>> x = Symbol('x')
>>> y = exp(-(x)**2/2)/sqrt(2*pi)
>>> Integral(y, (x, 0, 1)).evalf()
0.341344746068543
>>> Integral(y, (x, -1, 0)).evalf()
0.341344746068543
>>> Integral(y, (x, -1, 1)).evalf()
0.682689492137086
>>>

なのでy軸に対して対称性のある正規分布関数などを積分する場合は次のようなことができます。

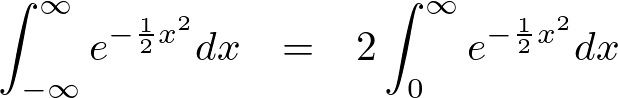
逆に非対称ではこういったことはできません。
このような性質を使って求める場合があり、例えばガンマ関数の1/2の場合の積分値などがあります。

ガンマ関数２分の１の例

次のように表現される式、

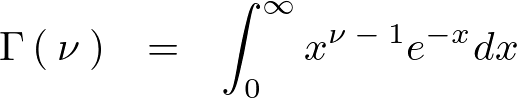
これを(ガンマ)関数といいます。この関数の変数部分が、

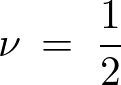
の場合を計算してみましょう。

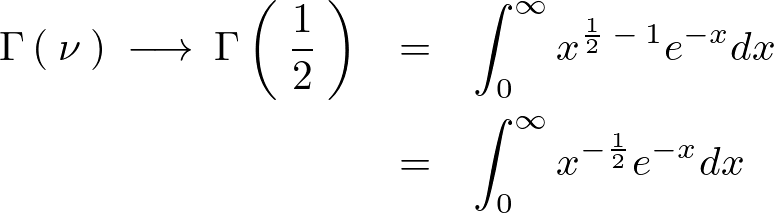
ここで次のような変数変換をします。

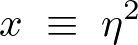
これを代入して計算していきますが、途中の式で先ほどの正規分布関数の性質を応用して０から無限大への積分範囲を、マイナスの無限大からプラスの無限大に拡大します。もちろん２倍になるので同値にするために２分の１を式中に付け足します。

最後はガウス積分の公式、

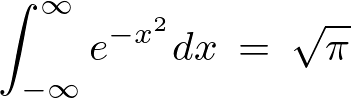
を使っています。 結果的に次のような公式が導かれます。

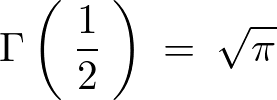
これ以外にも典型的な関係式を挙げると次のようなものがあります。

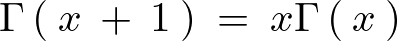
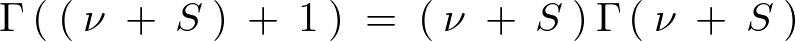
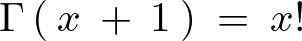
ガンマ関数の数値計算と描画

最初に次のようにインポートしてガンマ関数を認識させます。

from math import gamma

これを使って先ほどの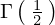を計算してみましょう。

次のように入力していきます。

from math import gamma
x1 = gamma(1/2)
print(x1)

そうすると以下のように出力されます。

>>> from math import gamma
>>> x1 = gamma(1/2)
>>> print(x1)
1.7724538509055159
>>>

ガンマ関数の描画

まず最初に次の物をインポートします。

from math import gamma #ここでgamma を認識させる
import numpy as np
import matplotlib.pyplot as plt

次にfrompyfuncを使ってユニバーサル関数に変換します。

gamma_func = np.frompyfunc(gamma, 1, 1)

座標データを格納します。

y = gamma_func(x)

ガンマ関数のグラフを描画するための処理箇所は以下のようになります。

fig = plt.figure(figsize = (8, 8))
ax = fig.add_subplot(111)
ax.set_title("Gamma function", size = 23)
ax.grid()
ax.set_xlim(0, 5.6)
ax.set_ylim(0, 15)
ax.set_xlabel("x", size = 16, labelpad = 10)
ax.set_ylabel("Gamma(x)", size = 16, labelpad = 10)
ax.plot(x, y)

全体としては次のように入力します。

from math import gamma #ここでgamma を認識させる
import numpy as np
import matplotlib.pyplot as plt

# x座標データを作成
x = np.linspace(0.01, 5.6, 350)

# frompyfuncを使ってユニバーサル関数に変換
gamma_func = np.frompyfunc(gamma, 1, 1)

# y座標データを作成
y = gamma_func(x)

# ガンマ関数のグラフを描画
fig = plt.figure(figsize = (8, 8))
ax = fig.add_subplot(111)
ax.set_title("Gamma function", size = 23)
ax.grid()
ax.set_xlim(0, 5.6)
ax.set_ylim(0, 15)
ax.set_xlabel("x", size = 16, labelpad = 10)
ax.set_ylabel("Gamma(x)", size = 16, labelpad = 10)
ax.plot(x, y)
plt.show()

次のような画像が出力されます。

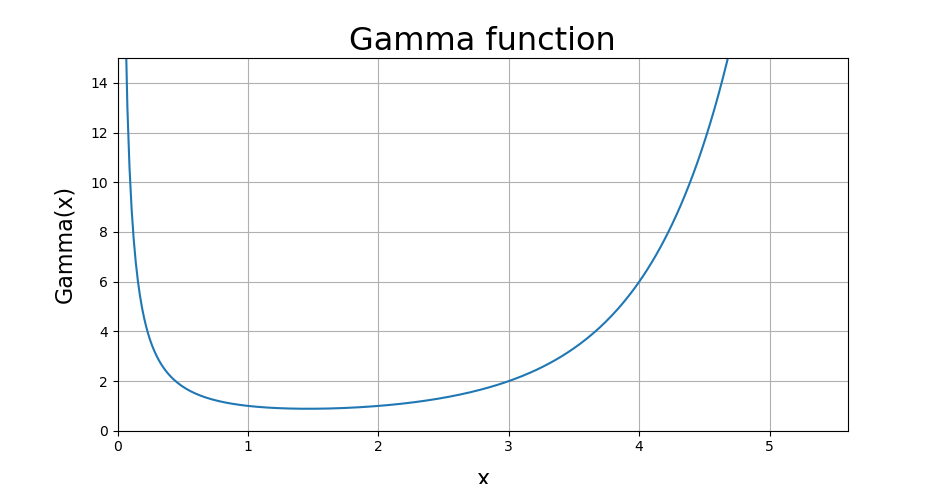
なおガンマ関数の描画に関しては以下のサイト様を参考にさせていただきました。

https://python.atelierkobato.com/gamma