Pythonによる3次元描画
新端末に変更して以来、旧端末でできていたことができなかったことなどがいくつかあり、ここではその対処法に関して解説していきます。
懸垂線の描画
ロープや糸など、ひもの類をその両端を固定して吊り下げたものを懸垂線などといいます。 これは物理的なポテンシャルが最小になるときのものであり、指数関数の![]() を使って次のような式で表されるものです。
を使って次のような式で表されるものです。
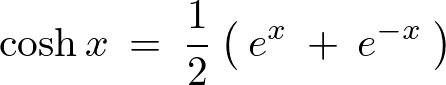
一般的にはコッシュ、またはハイパボリックコサインなどという呼び方をします。
ccosh(コッシュ),又はハイパボリックコサインの描画
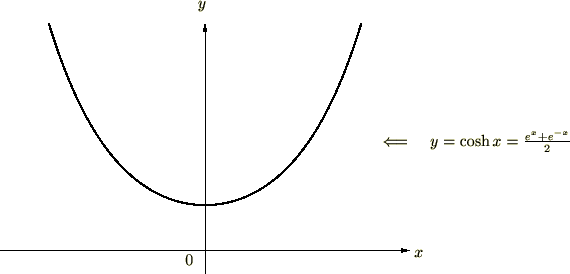
なおこれの導出の仕方については姉妹サイト微分方程式いろいろというサイトのこちらで詳しく説明していますのでご興味のある方は是非ご覧ください。
これをpythonで描画していきます。
import numpy as np import matplotlib.pyplot as plt x = np.arange(-1, 1, 0.001) y = np.cosh(x) plt.plot(x,y) plt.show()
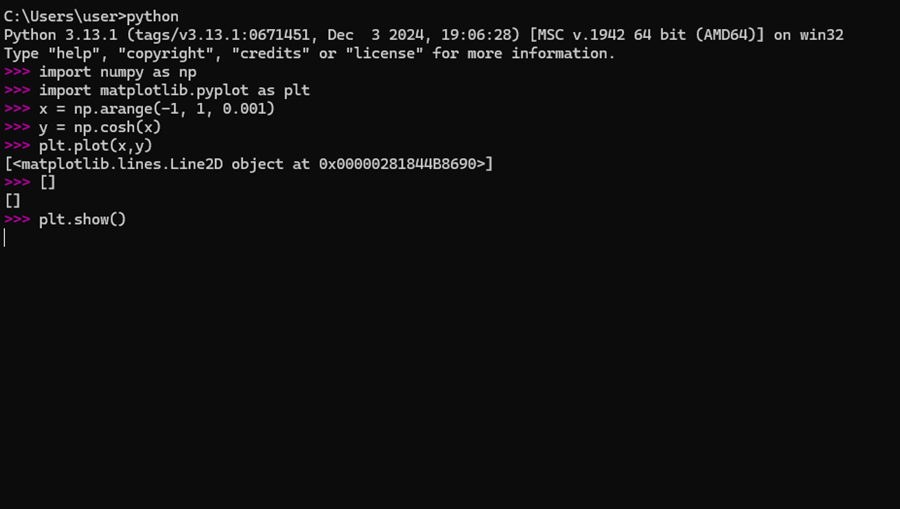
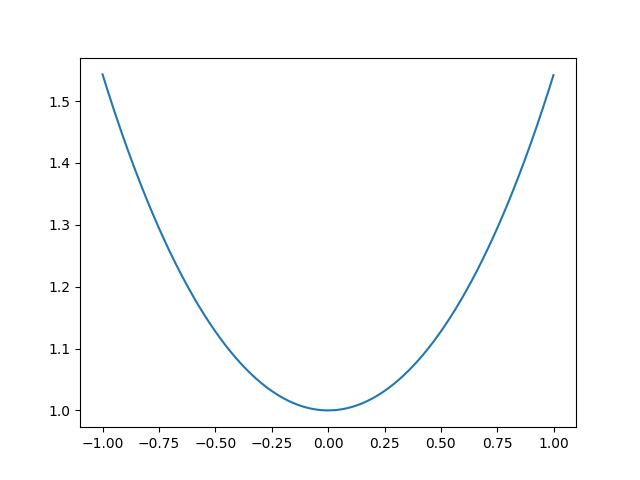
plt.show()と入力しEnterキーを押せば次のように出力されます。
sinh(シンチ)、またはハイパボリックサイン
先ほどのcoshに対してsinhなどと呼ばれるものもあり、同じように指数関数を使って次のような式で表せるようなものになります。
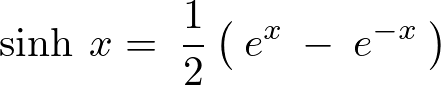
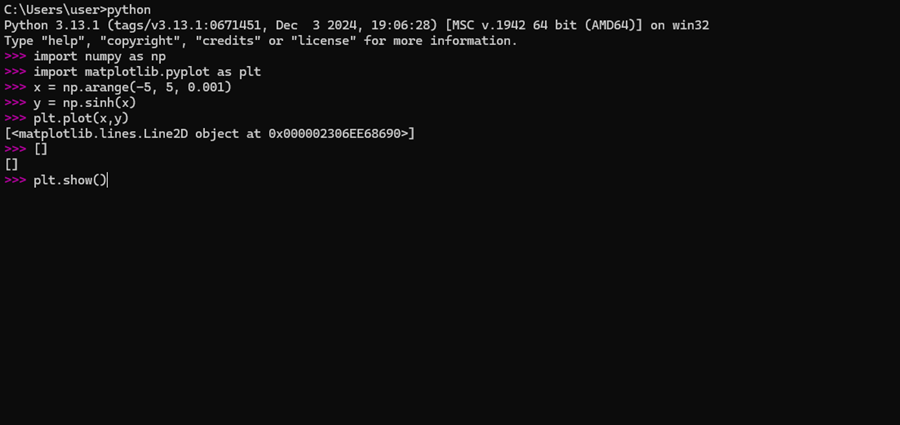
以下のように入力していきます。
import numpy as np import matplotlib.pyplot as plt x = np.arange(-5, 5, 0.001) y = np.sinh(x) plt.plot(x,y) plt.show()
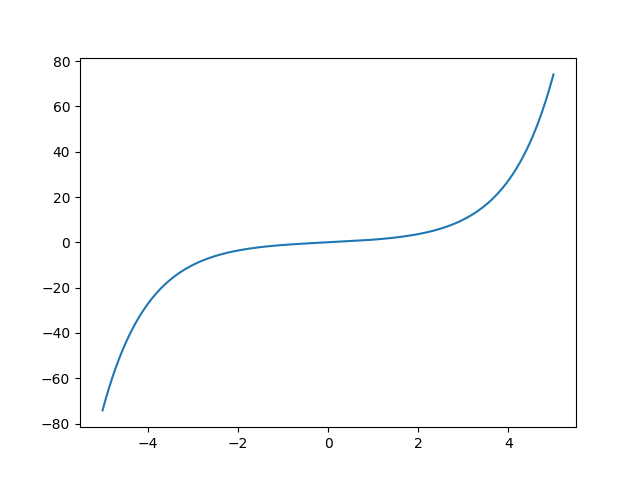
3次元描画
3次元の描画を行うには次のような3Dに関するインポートを行います。
from mpl_toolkits.mplot3d import Axes3D
先ほどのcoshの2次元画像に手を加えたものを描画してみます。なお依然の端末のPythonでは以下のコードで三次元描写ができていました。
from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np x = np.arange(-1, 1, 0.25) y = np.arange(-1, 1, 0.25) x, y = np.meshgrid(x, y) z = np.cosh(x)*np.cos(y) fig = plt.figure() ax = Axes3D(fig) ax.plot_wireframe(x,y,z) plt.show()
上記の最後のplt.show()でEnterを押下すればきれいな3次元画像が描写されていたのですが最新のPythonだと以下のように何も描写がされないという現象が出てしまいます。
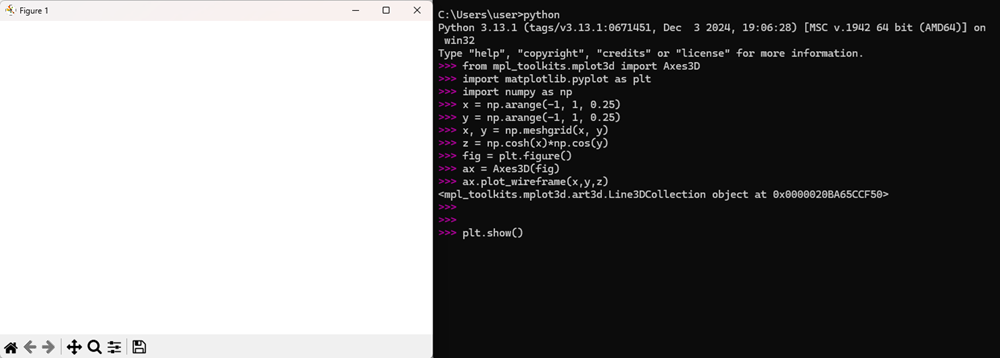
通常の場合ax = Axes3D(fig)でAxes3Dオブジェクトを生成して自動的にFigureオブジェクトが追加されるはずですが最新バージョンのものだとそれができないようです。
matplotlib公式ドキュメント
以下公式ドキュメントには以下のように記述されています。
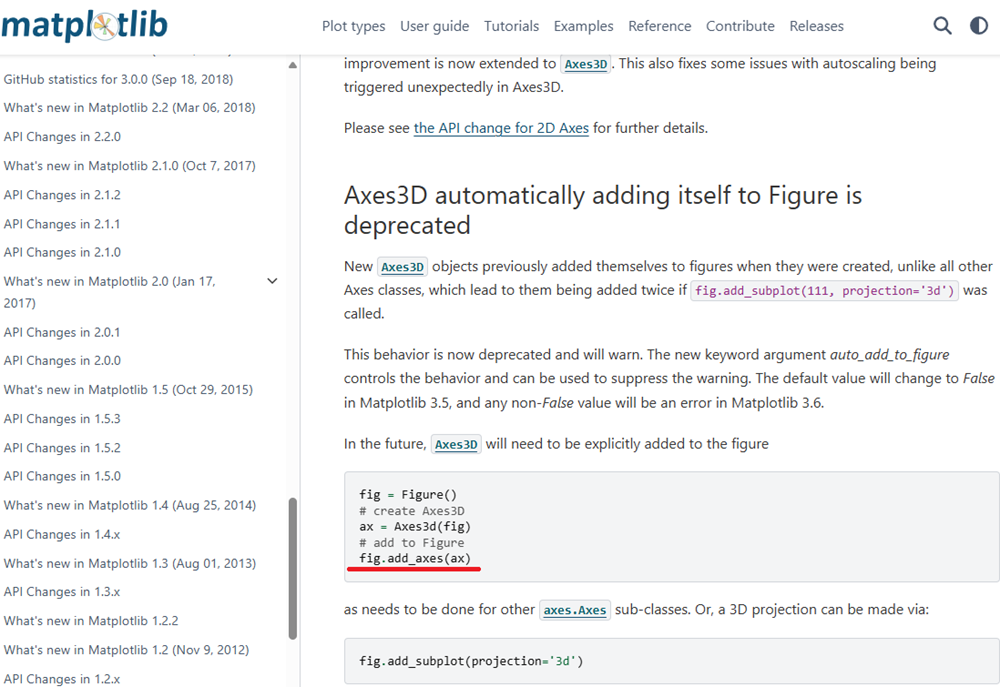
コメントアウトで# add to Figureとあり、その下にfig.add_axes(ax)を追加する旨が書いてあるので実際にこれの通りに追記して記述します。先ほどのコードにこのfig.add_axes(ax)を追記してコーディングします。
以下のようにして追記をします。
from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np x = np.arange(-1, 1, 0.25) y = np.arange(-1, 1, 0.25) x, y = np.meshgrid(x, y) z = np.cosh(x)*np.cos(y) fig = plt.figure() ax = Axes3D(fig) fig.add_axes(ax)#この部分が付加箇所 ax.plot_wireframe(x,y,z) plt.show()
すると以下のように先ほどは全く表示されなかったものがきれいな三次元による描画ができるようになります。
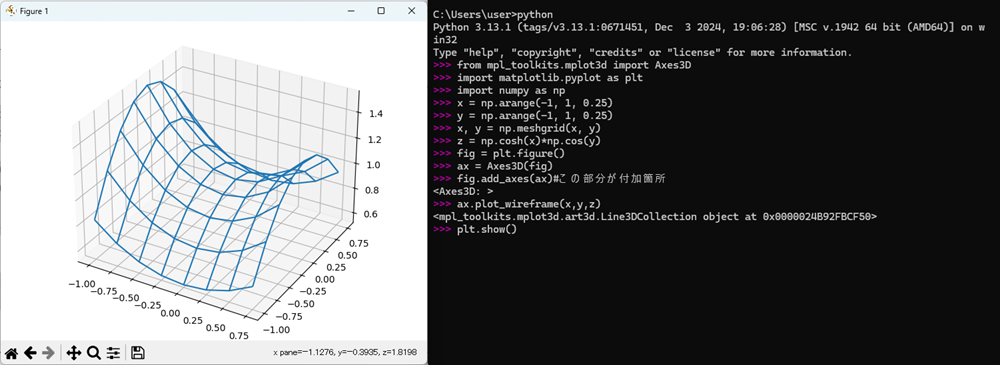
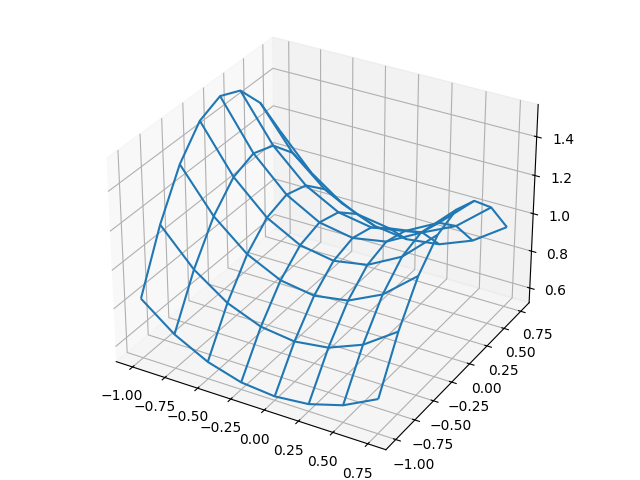
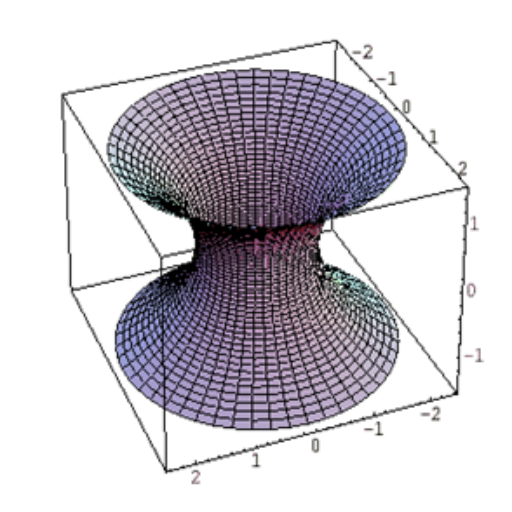
懸垂面の描画
今度は先ほどの画像にもうちょっと手を加えたものを描画してみましょう。
次のように打ち込んでいくか、でなければコードの部分を全部コピペしてEnterを押します。
from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np u = np.linspace(0, 2*np.pi, 50) v = np.linspace(-1, 1, 50) x = np.outer(np.cosh(v), np.cos(u)) y = np.outer(np.cosh(v), np.sin(u)) z = np.outer(v, np.ones_like(u)) fig = plt.figure() ax = Axes3D(fig) fig.add_axes(ax)#この部分が付加箇所 ax.plot_wireframe(x,y,z) plt.show()
以下のようなきれいな3次元描画が実行されます。
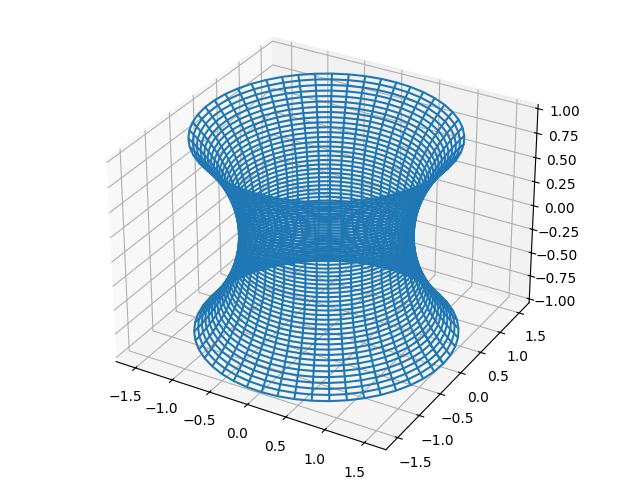
これは懸垂面と呼ばれるものになり、これの特徴的なところはいたるところで平均曲率が0になるというものになります。
-
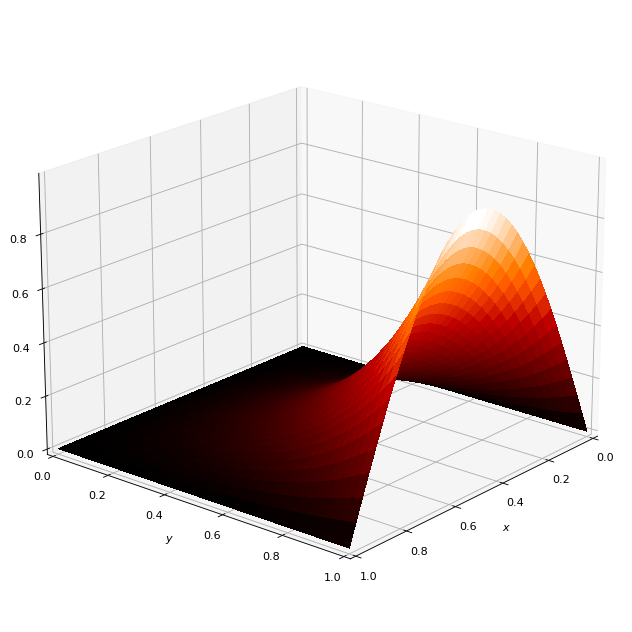
ラプラス方程式Pythonコード
続きを読む
-
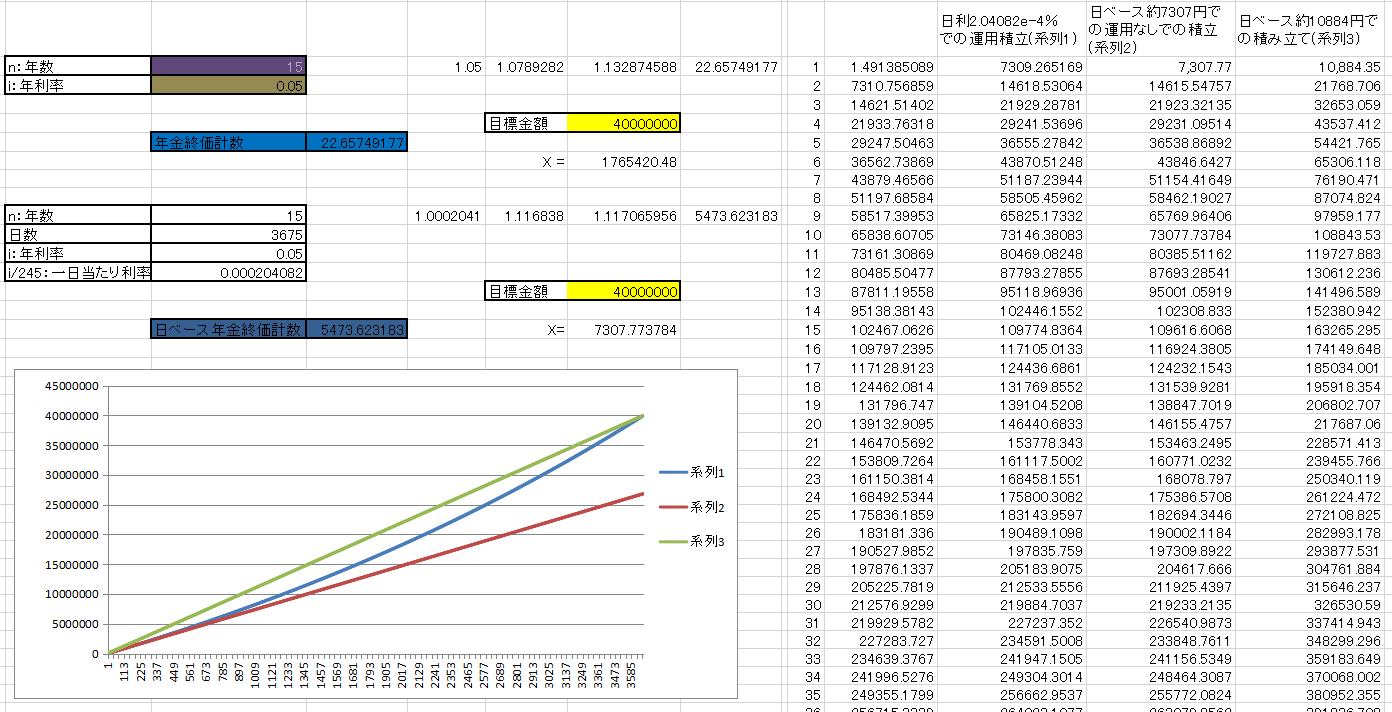
つみたてNISAと年金終価係数
続きを読む
-
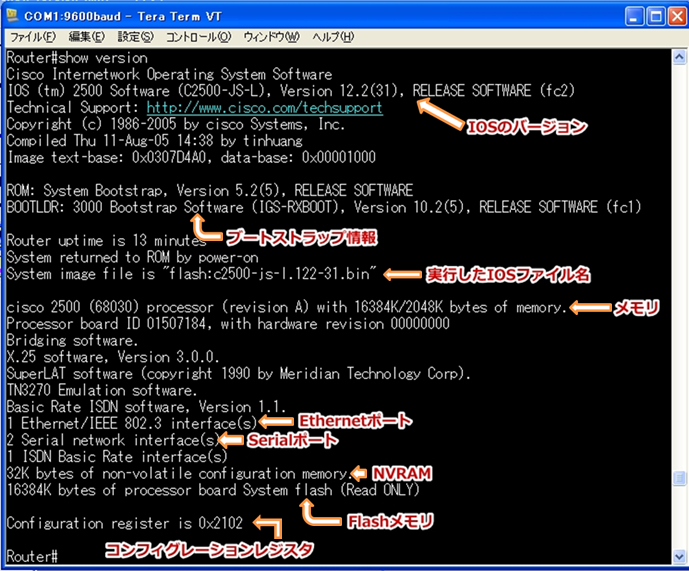
ルータ1台の基本設定
続きを読む
-
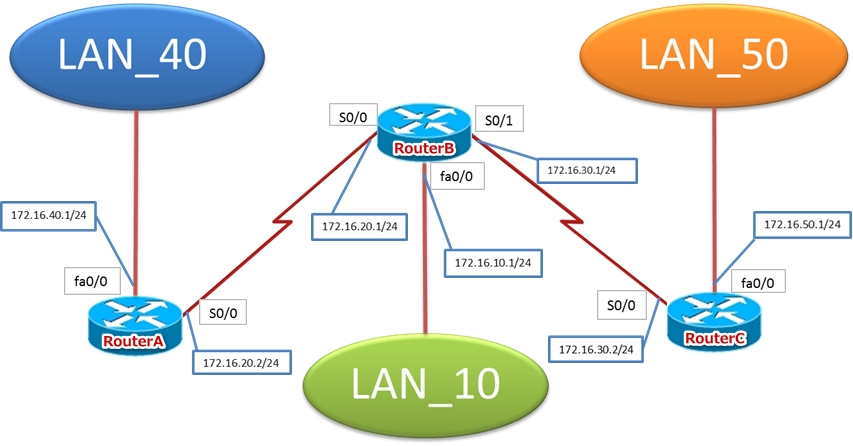
スタティックルーティング
続きを読む
-

IPルーティング
続きを読む
-
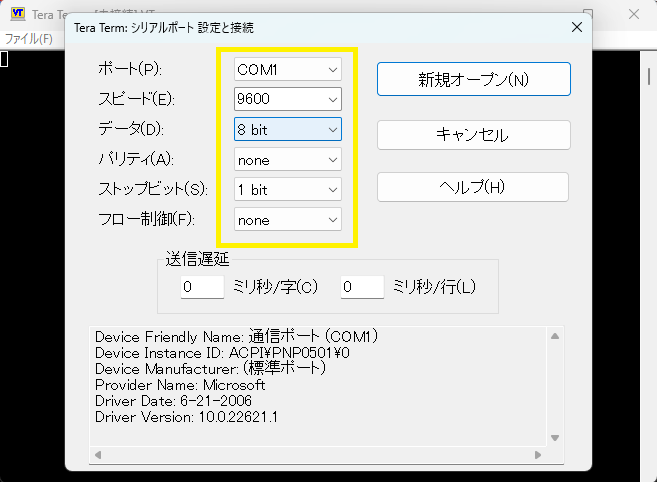
テラタームの設定
続きを読む
テスト投稿
-

ラプラス方程式Pythonコード
続きを読む
-

つみたてNISAと年金終価係数
続きを読む
-

ルータ1台の基本設定
続きを読む
-

スタティックルーティング
続きを読む
-

IPルーティング
続きを読む
-

テラタームの設定
続きを読む