RグラフィックとTeXへの取り込み
統計数学やファイナンス数学などにおいてよく使われる関数に正規分布関数と言われるものがあります。 以下のような数式によって表せられるものになります。
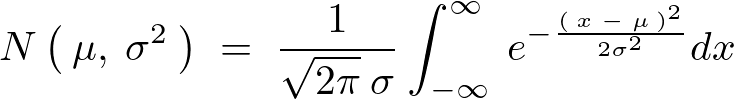
正規分布関数
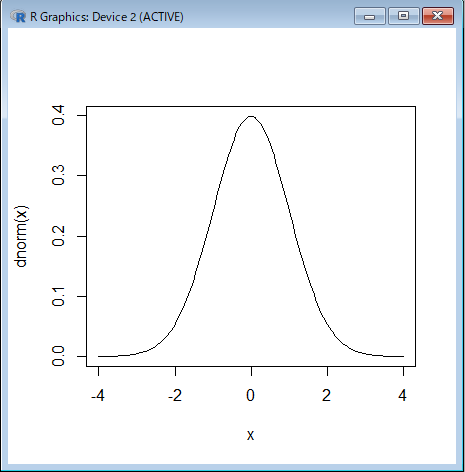
左の画像はRを使って描画した正規分布関数です。
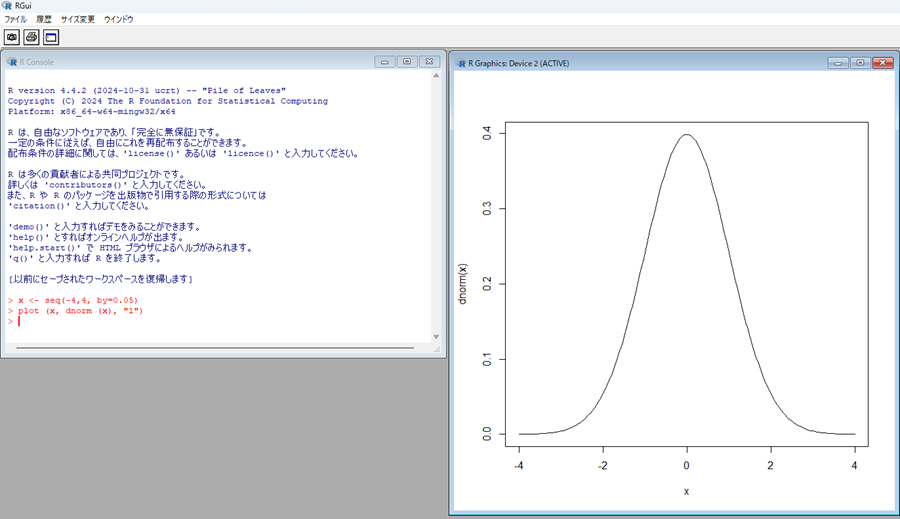
このような画像を出力するには次のようにコードを入力していきます。
x <- seq(-4,4, by=0.05)
のように入力してEnterキーを押します。次に、
plot (x, dnorm (x), "l")
と入力してEnterキーを押せば次のように簡単に正規分布関数のグラフが出力されます。
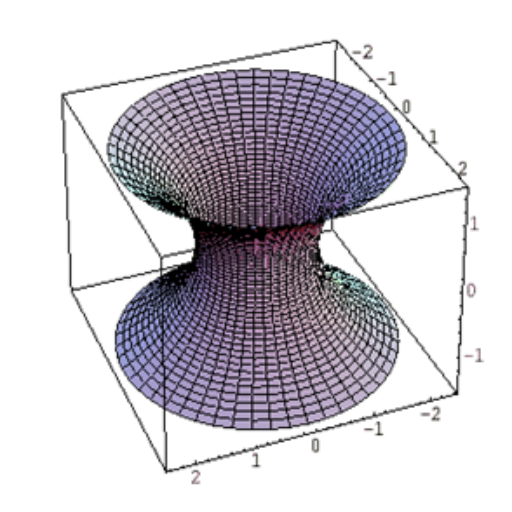
3次元描画
x <- seq(-4,4, by=0.05)
plot (x, dnorm (x), "l")
x <- seq (-4,4,length=50)
<- seq (-4,4,length=50)
gauss3d <- function (x,y) {dnorm (x) *dnorm (y)}
z <- outer (x,y,gauss3d)
persp(x,y,z,expand=0.7)
すると次のように描画されます。
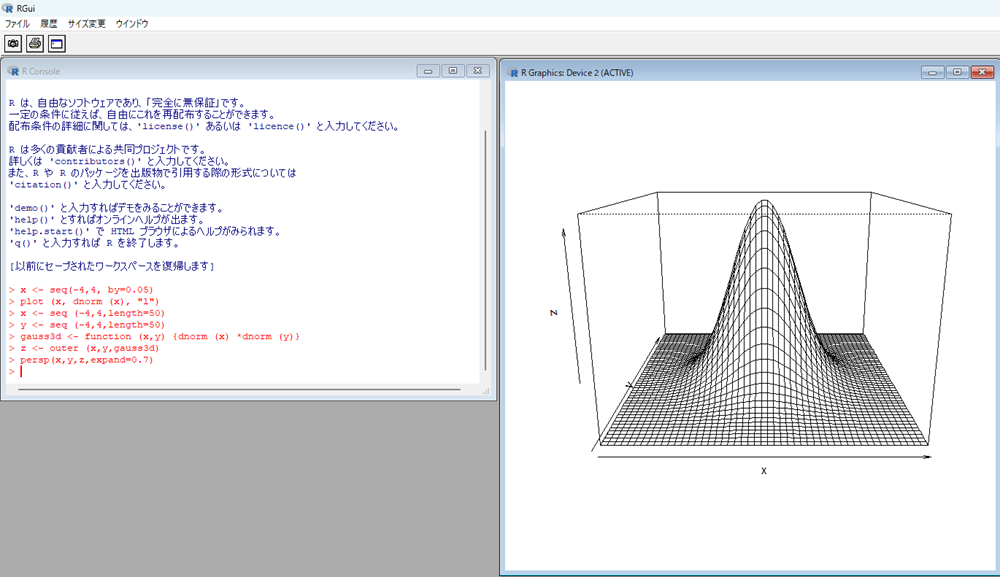
ポアソン分布
その他関数も組み込まれています。
例えばポアソン分布(λ=1)、
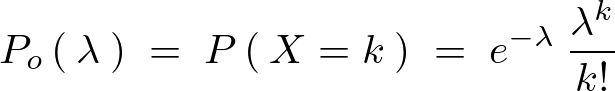
は次のように打ち込むと右図のように描画されます。
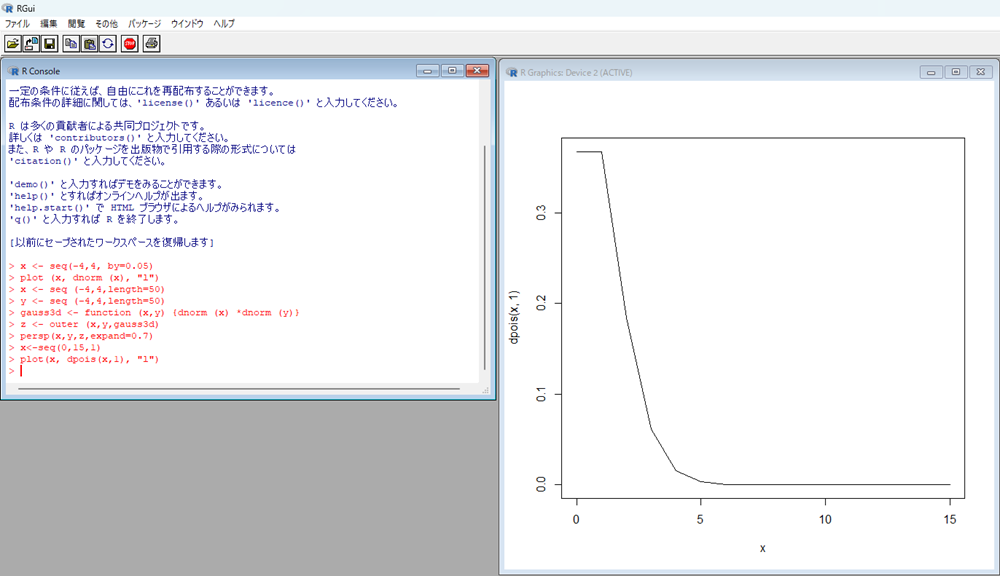
2項分布
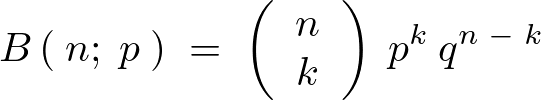
上記の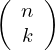 は、
は、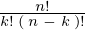 の簡略表記で、式中の
の簡略表記で、式中の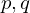 は
は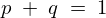 の関係にあります。
の関係にあります。
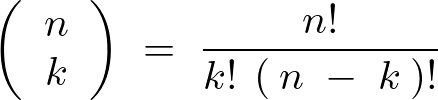
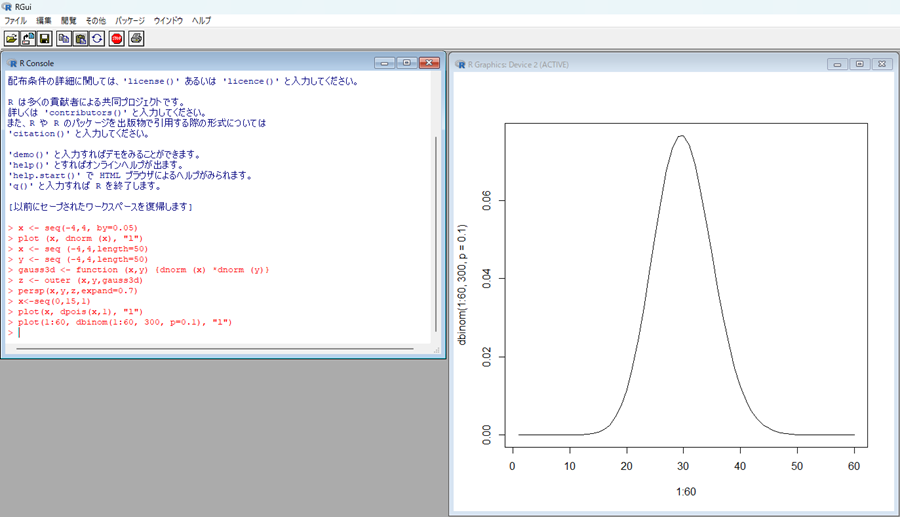
plot(1:60, dbinom(1:60, 300, p=0.1), "l")
ポストスクリプト出力
ファイル出力においてはポストスクリプトの.eps出力もできます。
TeXファイルに画像を組み込むときこの種類の拡張子ファイルが必要になります。
ひとまず最初に画像をコーディングします。
x <- seq (-4,4,length=50)
y <- seq (-4,4,length=50)
gauss3d <- function (x,y) {dnorm (x) *dnorm (y)}
z <- outer(x, y, gauss3d)
persp(x, y, z, expand = 0.7, theta = 50, phi = 30, col = "yellow")
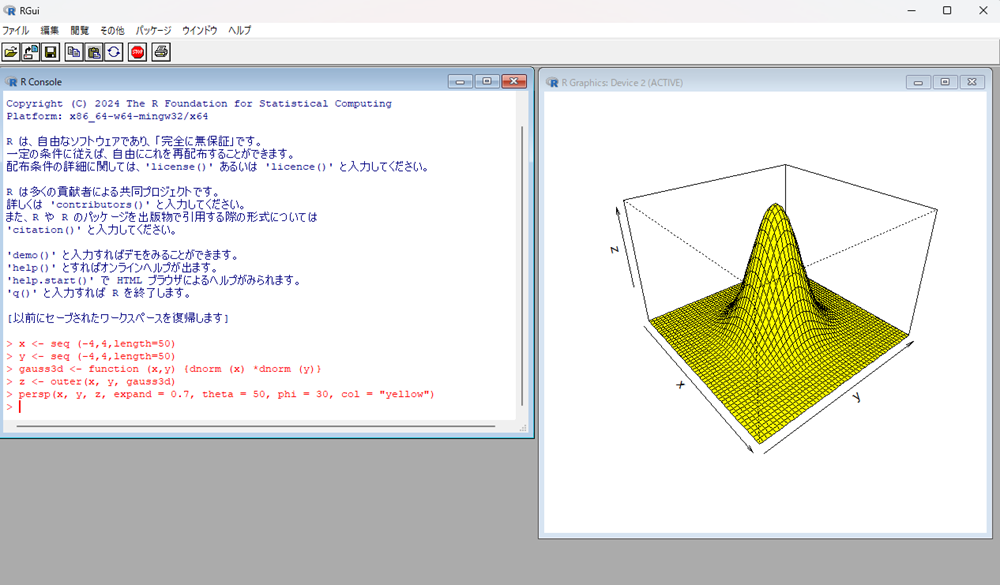
Enterを押下して画像を出力し、そのあと画像の出ているフレーム内のどこかをクリックします。
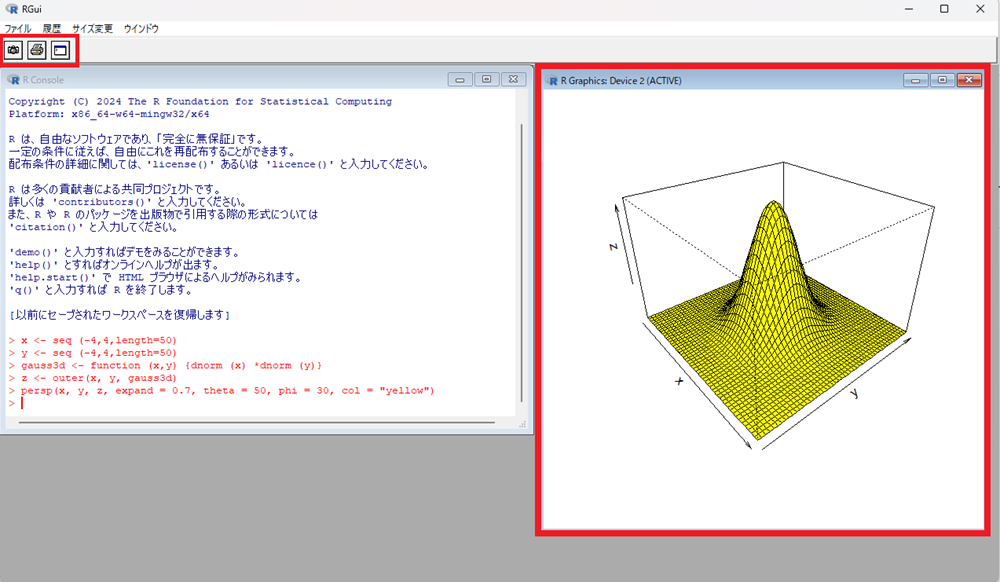
そうするとリボンバーの表示が変わりますのでその時にファイルのタブをクリックします。
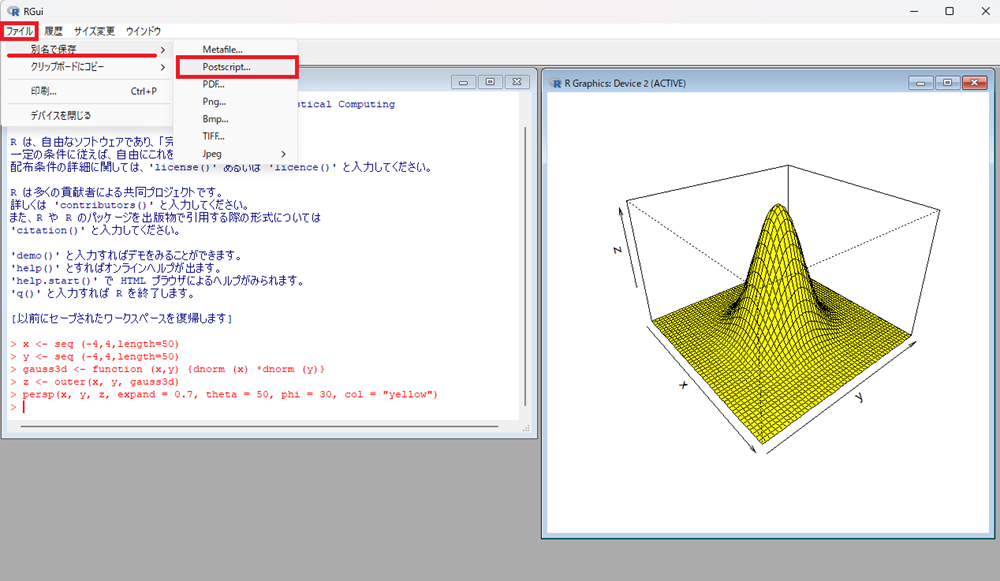
上のようにプルダウンが出てくるのでその中のPostscriptをクリックすると、指定したフォルダ(ディレクトリ)上にGSviewのアイコンが作成表示されます。
TeXファイルへの取り込み
\chapter{モーメント母関数}
ある確率変数$X$に対して、$e^{tX}$の期待値を$X$のモーメント母関数(積率母関数)と言います。
\
\begin{picture}(0,0)
\begin{LARGE}$M_X\left(\:t\:\right)\:=\:\int^{\infty}_{-\infty}e^{tX}\:f_X\left(\:x\:\right)\:dx$\end{LARGE}
\end{picture}
\[
M_X\left(\:t\:\right)\:=\:\int^{\infty}_{-\infty}e^{tX}\:f_X\left(\:x\:\right)\:dx
\]
\section{正規分布関数}
\[
N\left(\:\mu,\:\sigma^2\:\right)\;=\;\frac{1}{\sqrt{2\pi}\:\sigma}\int^{\infty}_{-\infty}\:e^{-\frac{\left(\:x\;-\;\mu\:\right)^2}{2\sigma^2}}dx \]
\vspace{300pt}
\
\begin{picture}(0,-50)
\includegraphics{nomal_distribution_rstuido_output_2024img.eps}%←この部分が画像を指定するコード
\end{picture}
上記の、\includegraphics{nomal_distribution_rstuido_output_2024img.eps}と書かれている部分が取り込みのための記述になります。
ファイルの置き場所が違う場合はパスコードを追加して指定してください。
最後にplatex~でコンバーティングして出力させれば次のようにDVIファイル上にRで作成した画像が取り込まれます。
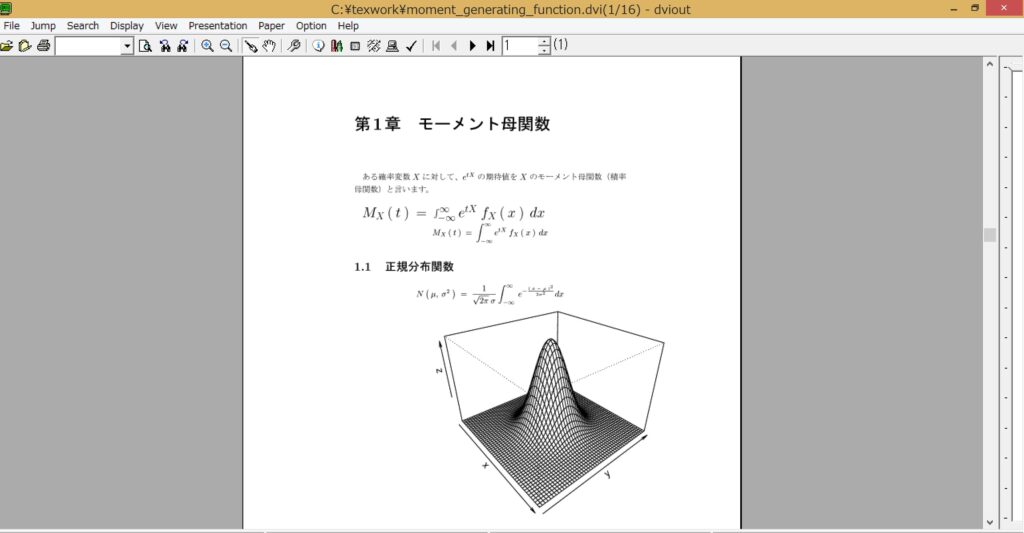
-
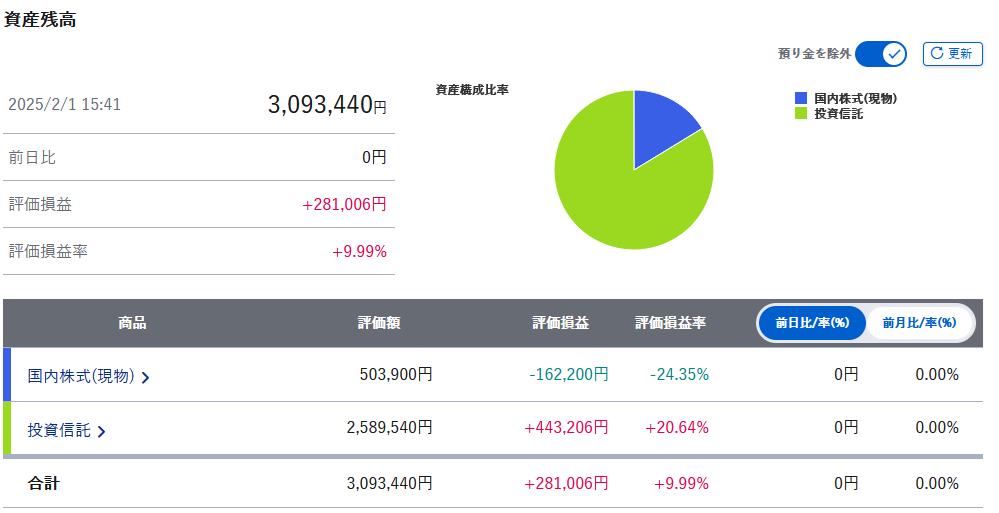
2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-
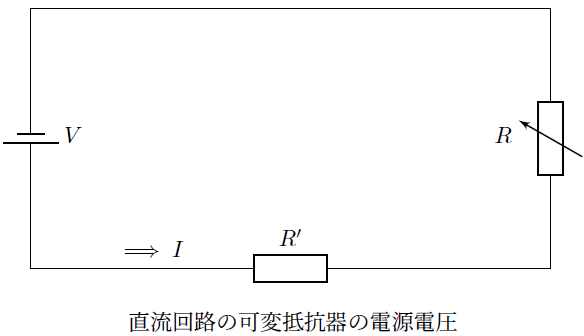
可変抵抗器の直列回路
続きを読む
-
Packet Tracer
続きを読む
-
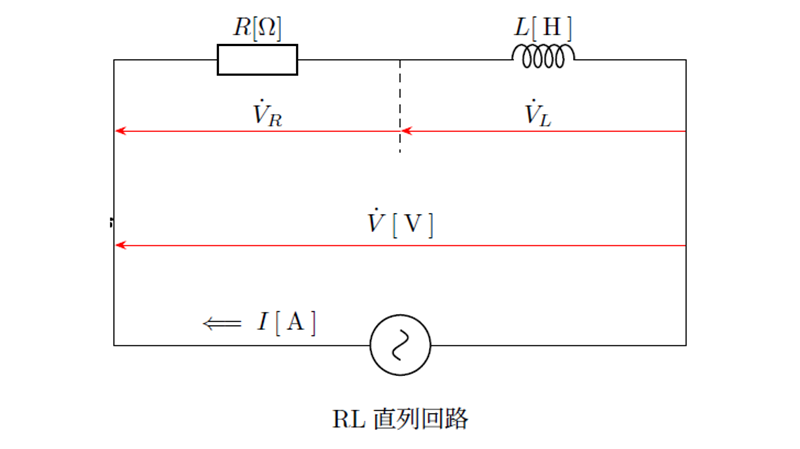
交流回路の直列接続
続きを読む
-
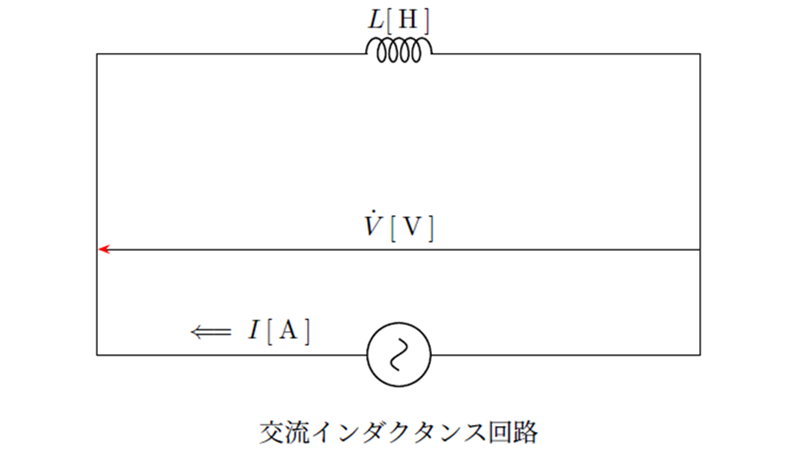
交流回路
続きを読む
テスト投稿
-

2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-

可変抵抗器の直列回路
続きを読む
-

Packet Tracer
続きを読む
-

交流回路の直列接続
続きを読む
-

交流回路
続きを読む