微分方程式LaTeXコード
微分方程式いろいろ コード
コード
サテライトサイト微分方程式いろいろコンテンツトップページに使われた コードになります。コンパイル時のエラー等の修正は確認済みなのでこのまま自端末の
コードになります。コンパイル時のエラー等の修正は確認済みなのでこのまま自端末の 文書にコピペして貼り付けてDVIファイル出力すれば同様の数式画像が得られます。
文書にコピペして貼り付けてDVIファイル出力すれば同様の数式画像が得られます。
基本的に管理人の備忘録用のログとして作成していますが関連するキーワードで該当するものがあれば学習教材を作成するなどした場合に利用できると思います。
ただし近年コンテンツ盗用がかなり目立ちます。参考にしたのであれば紹介リンクを貼るなどの対応は必ずお願いいたします。
微分方程式例題1
 コード
コード
\[
ay^2\:=\:\left(\:x\:+\:b\:\right)
\]
\begin{eqnarray*}
a\frac{d}{dx}\left(y^2\right)&=&3\frac{d}{dx}\left(x+b\right)\\
a\frac{dy}{dx}\frac{dy^2}{dy}&=&3\frac{d}{dx}x\;+\;3\frac{d}{dx}b\\
2ay\frac{dy}{dx}&=&3
\end{eqnarray*}
出力画像

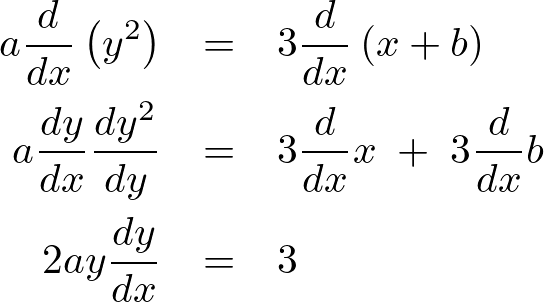
 コード
コード
\begin{eqnarray*}
2a\frac{d}{dx}\left(\:y\frac{dy}{dx}\:\right)=\frac{d}{dx}3\\
\end{eqnarray*}
\begin{eqnarray*}
2a\frac{dy}{dx}\cdot\frac{dy}{dx}\;+\;2ay\frac{d^2y}{dx^2}\;=\;0\\
\end{eqnarray*}
\begin{eqnarray*}
2a\left(\:\frac{dy}{dx}\:\right)^2\;+\;2ay\frac{d^2y}{dx^2}=\;0\\
\end{eqnarray*}
\begin{eqnarray*}
\left(\:\frac{dy}{dx}\:\right)^2\;+\;y\frac{d^2y}{dx^2}\;=\;0
\end{eqnarray*}
\begin{eqnarray*}
\frac{d^2y}{dx^2}\;=\;-\frac{1}{y}\left(\:\frac{dy}{dx}\:\right)^2
\end{eqnarray*}
出力画像

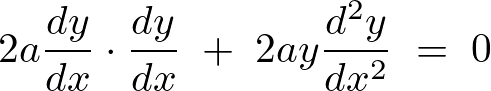
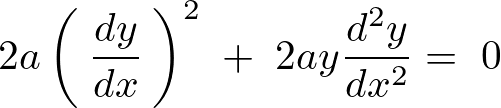
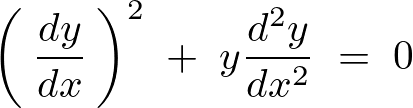
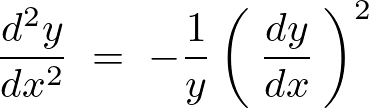
微分方程式例題2(円に関する考察)
 コード
コード
\begin{eqnarray*}
x^2\:+\:y^2\:=\:c\quad\left(\:c\:>\:0\right)
\end{eqnarray*}
\begin{eqnarray*}
\frac{d}{dx}x^2\;+\;\frac{d}{dy}y^2\;=\;\frac{d}{dx}c
\end{eqnarray*}
\begin{eqnarray*}
\frac{dx^2}{dx}+\frac{dy^2}{dy}\frac{dy}{dx}=0\\
\end{eqnarray*}
\begin{eqnarray*}
2x+2y\frac{dy}{dx}=0\\
\end{eqnarray*}
\begin{eqnarray*}
\frac{dy}{dx}=-\frac{x}{y}
\end{eqnarray*}
出力画像

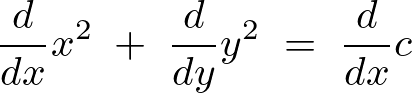
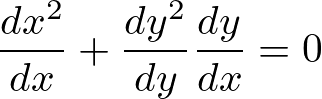
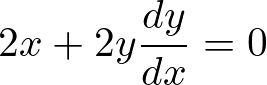
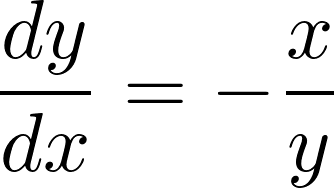
微分方程式例題3(力学への応用)
 コード
コード
\begin{eqnarray*}
dE=0\qquad\left(\frac{dE}{dt}=0\right)
\end{eqnarray*}
\begin{eqnarray*}
dE&\;=\;&\frac{\partial E}{\partial \dot{y}}d\dot{y}\:+\:\frac{\partial E}{\partial y}dy
\end{eqnarray*}
\begin{eqnarray*}
\frac{\partial E}{\partial \dot{y}}=m\dot{y}\quad&&\frac{\partial E}{\partial y}=mg
\end{eqnarray*}
\begin{eqnarray*}
dE&=&m\dot{y}d\dot{y}\:+\:mgdy\\
&=&m\frac{dy}{dt}\left(d\frac{dy}{dt}\right)+mg\:dy
\end{eqnarray*}
\begin{eqnarray*}
\frac{dE}{dt}&=&m\frac{dy}{dt}\frac{d^2y}{dt^2}+mg\frac{dy}{dt}\\
&=&\left(m\frac{d^2y}{dt^2}+mg\right)\frac{dy}{dt}
\end{eqnarray*}
\begin{eqnarray*}
\frac{dE}{dt}&=&m\left(\frac{d^2y}{dt^2}+g\right)\frac{dy}{dt}\\
&=&0
\end{eqnarray*}
出力画像
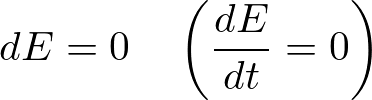


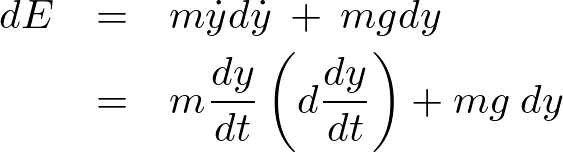
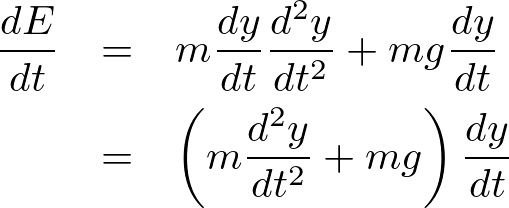

-
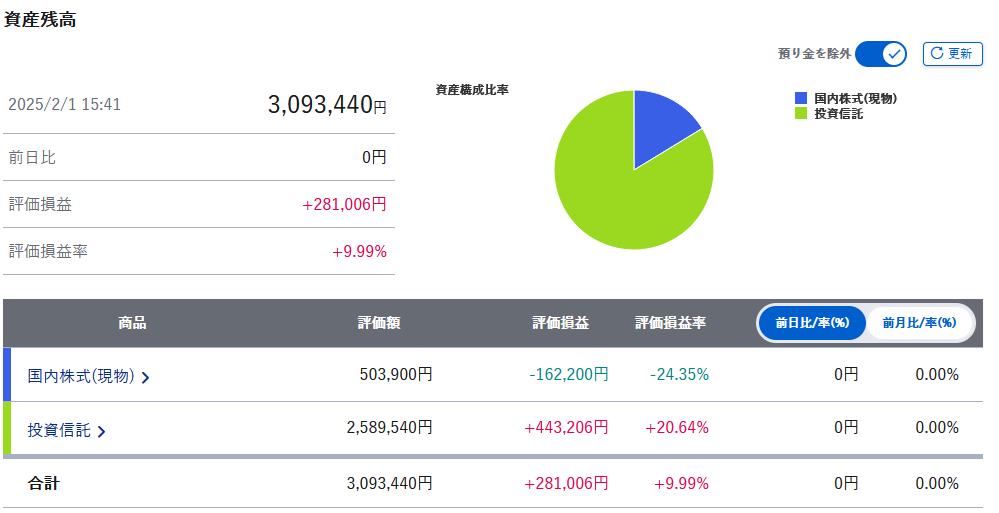
2025年1月NISA運用概況
カテゴリー
-

2025年1月金運用概況
カテゴリー
-
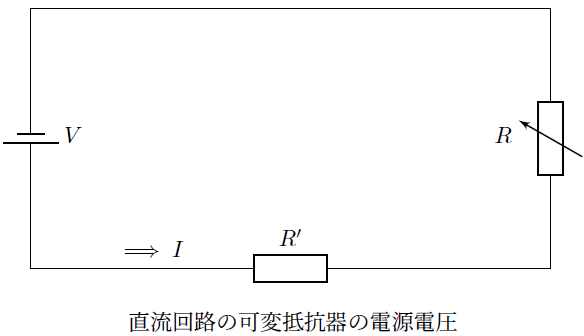
可変抵抗器の直列回路
カテゴリー
-
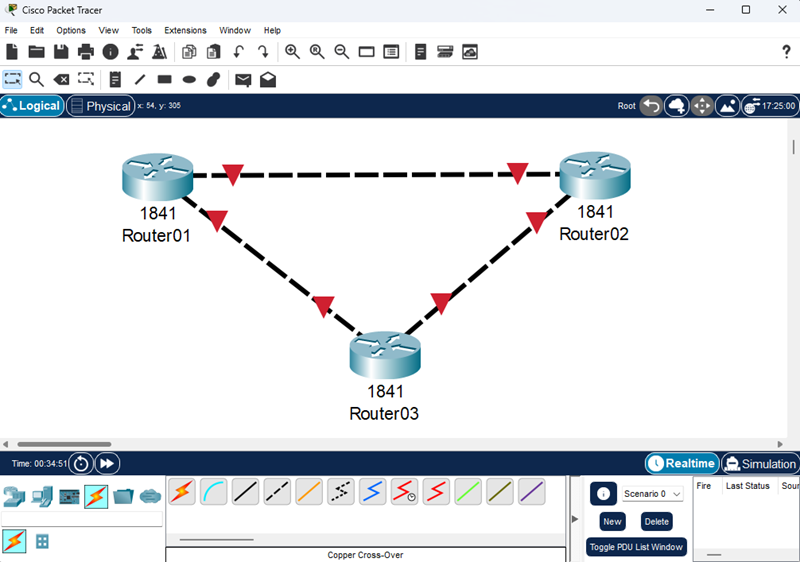
Packet Tracer
カテゴリー
-
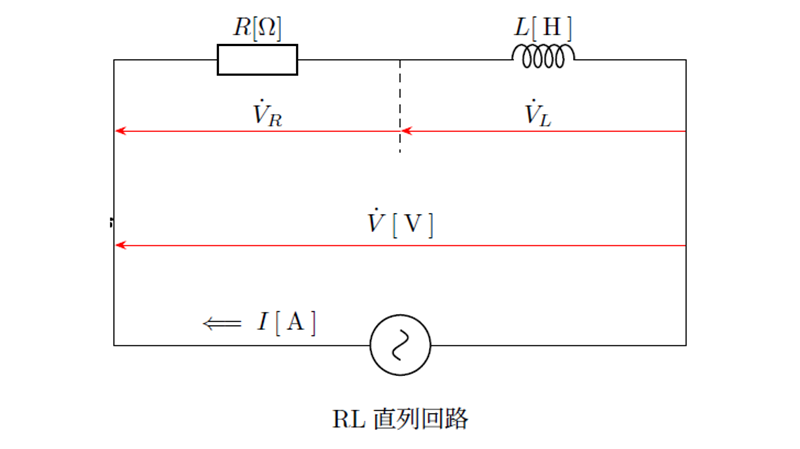
交流回路の直列接続
カテゴリー
-
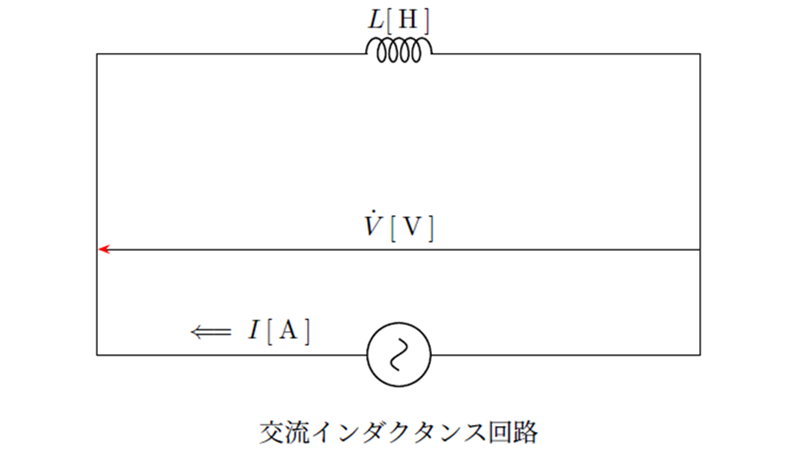
交流回路
カテゴリー
テスト投稿
-

2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-

可変抵抗器の直列回路
続きを読む
-

Packet Tracer
続きを読む
-

交流回路の直列接続
続きを読む
-

交流回路
続きを読む