オームの法則
![]() を電流、
を電流、![]() を電圧、
を電圧、![]() を抵抗とおくと、これらの変数は以下のような関係式によって成り立っていることがわかっています。
を抵抗とおくと、これらの変数は以下のような関係式によって成り立っていることがわかっています。
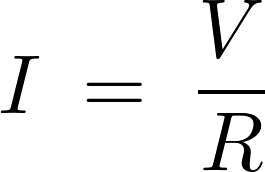
式を見てわかるように電流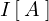 は加える電圧
は加える電圧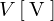 に比例し、抵抗
に比例し、抵抗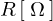 に反比例します。
に反比例します。
これを一般的にオームの法則と呼びます。
以下に示すような電源と抵抗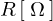 を考え、そしてその流れる電流を
を考え、そしてその流れる電流を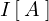 とします。
とします。
抵抗に電流が流れると、図の![]() の両端には、先ほどのオームの法則を変形した以下に示すような電位差が生じることになります。
の両端には、先ほどのオームの法則を変形した以下に示すような電位差が生じることになります。
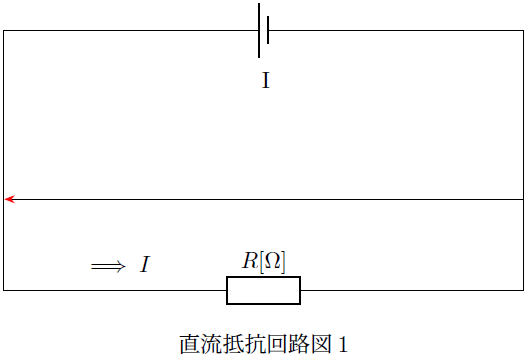
この電位差の式を電圧降下と言います。
ひとまずいえることはまず最初に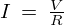 という式を完全に覚えてしまってから以下のように式変形していくという流れがいいような気がします。
という式を完全に覚えてしまってから以下のように式変形していくという流れがいいような気がします。
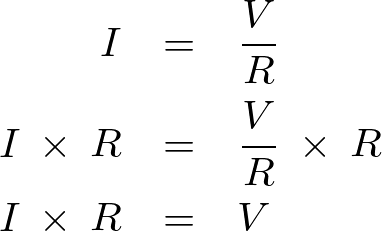
より、
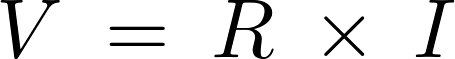
上記式をさらに変形させて、
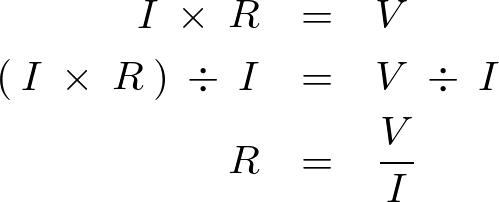
より、
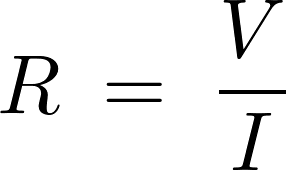
といった具合で式変形をしていくとそれぞれの式が導かれるのでとりあえずはまず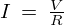 というオームの法則式自体を完全に覚えてしまったほうがいいように思います。
というオームの法則式自体を完全に覚えてしまったほうがいいように思います。
ex.
20![]() の抵抗に4
の抵抗に4![]() の電流が流れているとします。この時の電流は以下のようにして求められます。
の電流が流れているとします。この時の電流は以下のようにして求められます。
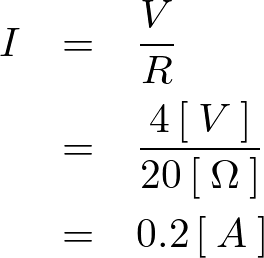
抵抗の直列接続
次に示すような直流回路における2個の抵抗が直列につながれた電気回路を考えます。
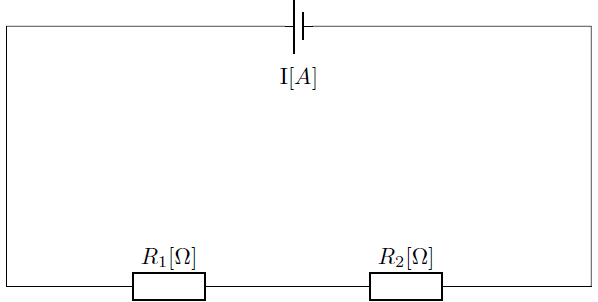
流れる電流は同じなので、
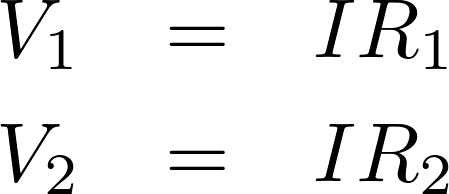
電源電圧は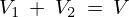 なので、
なので、
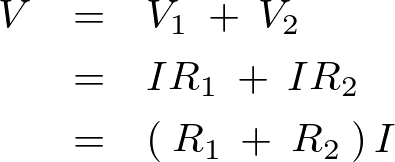
![]() なので、
なので、
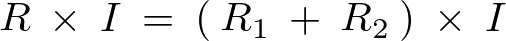
という等式が成り立つので、上記の両辺を![]() で割れば、直列接続の抵抗回路の式は以下のような関係式が求まることになります。
で割れば、直列接続の抵抗回路の式は以下のような関係式が求まることになります。
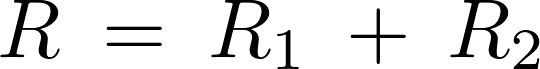
さらに直列に抵抗をつなげていった場合を考えます。
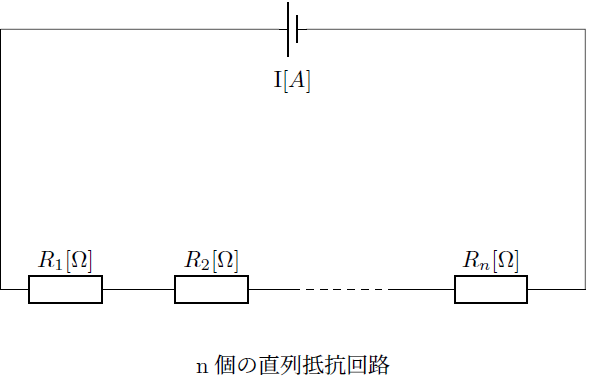
図のように![]() 個の抵抗値をつなげていった場合でも、結局のところその合成抵抗は各抵抗値の和となって表れるため次のように表現できることになります。
個の抵抗値をつなげていった場合でも、結局のところその合成抵抗は各抵抗値の和となって表れるため次のように表現できることになります。
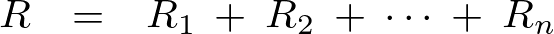
抵抗の並列接続
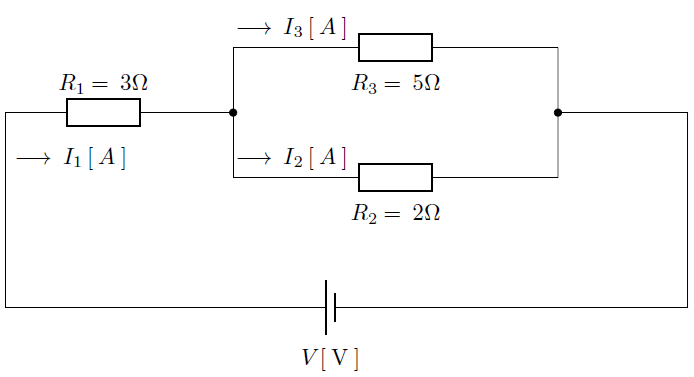
以下のような抵抗を配置した直流回路を考えます。
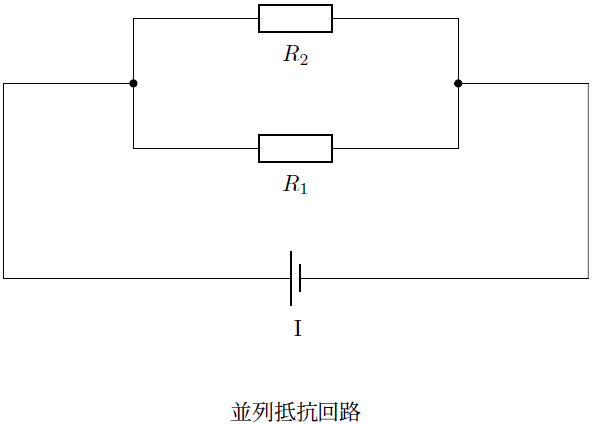
抵抗を並列につないでいるので並列接続になり、このときの並列抵抗回路では回路中のどの抵抗にも同じ大きさの電圧が加わります。
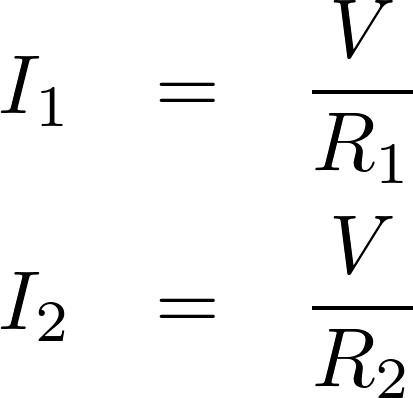
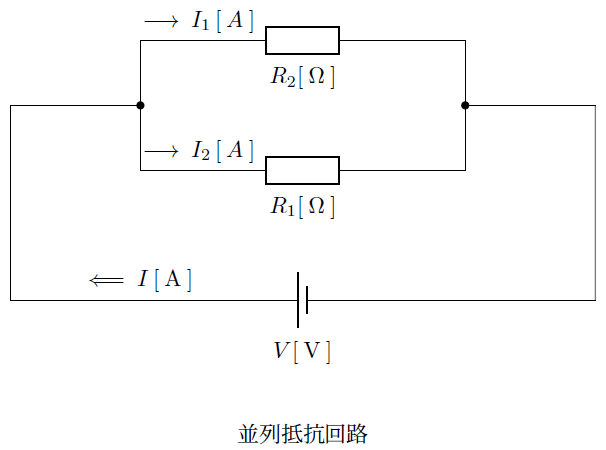
ここでキルヒホッフの法則より全電流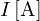 は
は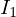 と
と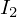 の合計になるので以下のような等式が成り立ちます。
の合計になるので以下のような等式が成り立ちます。
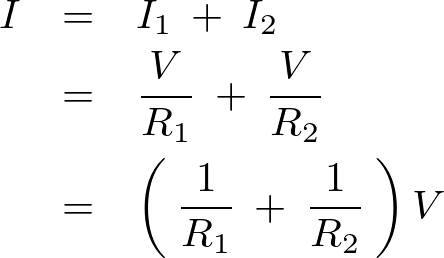
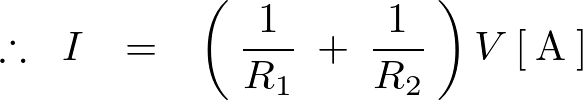
また先ほどの並列抵抗回路は以下のような回路図と同等のものと考えることができます。
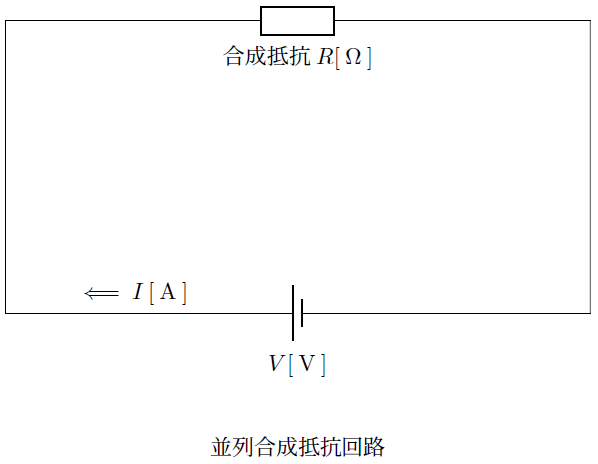
この回路図でのオームの法則は以下、
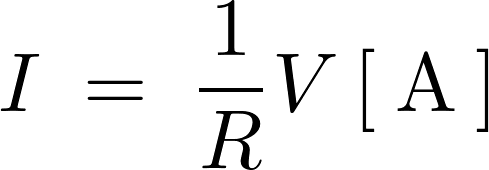
であるので、2つの抵抗を並列に接続した場合の抵抗値は以下のように表せることになります。
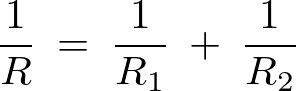
これを![]() に関して式を変形していけば次のように求まることになります。
に関して式を変形していけば次のように求まることになります。
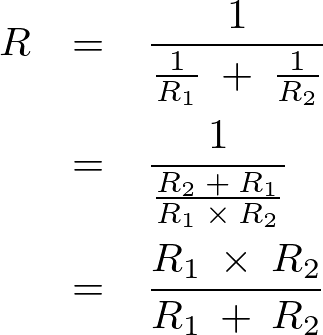
並列接続2個以上の場合
図のような2個以上の複数個の並列抵抗がある場合を考えます。
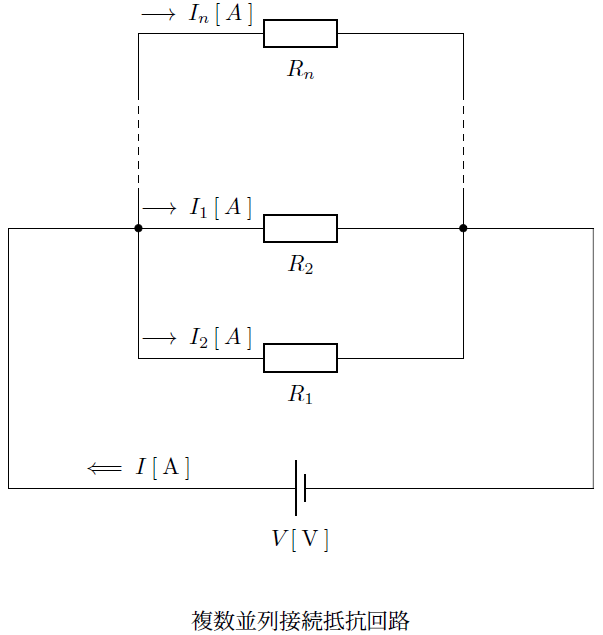
上記のようなn個の抵抗を並列接続した場合は次のようになります。
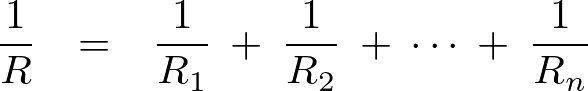
より、
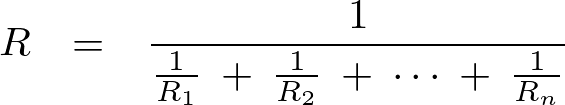
例題1
以下に示すような3列並列回路の抵抗を求めてみましょう。
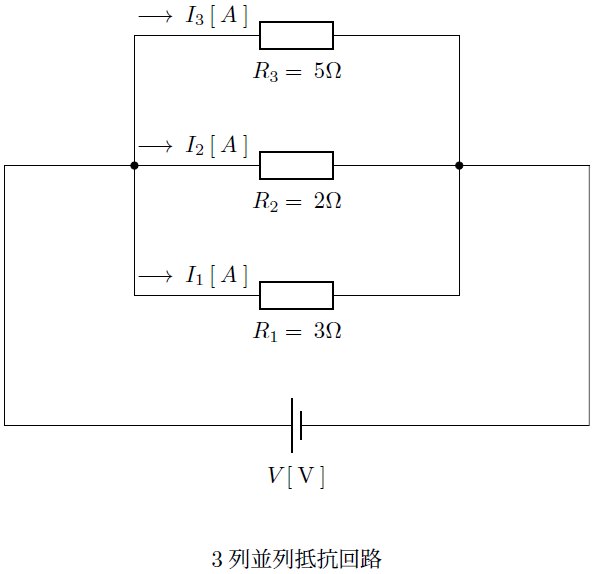
次のような計算になります。
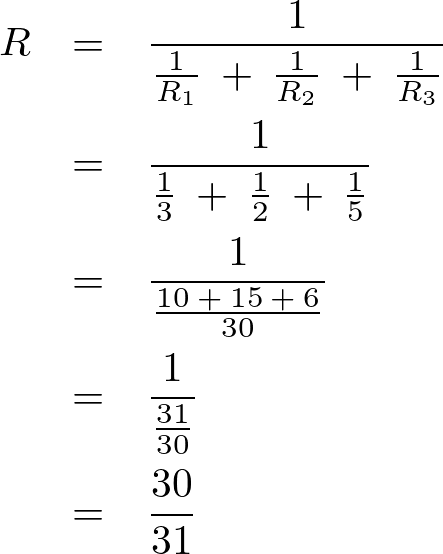
ゆえに上記3並列抵抗回路の合成抵抗値は以下のように求まることになります。
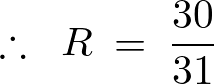
例題2
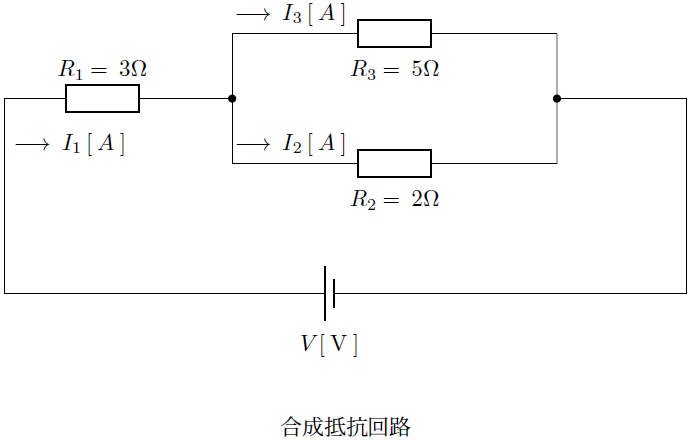
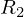 と
と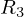 の並列合成抵抗値を求め、それを一つの抵抗とみなして
の並列合成抵抗値を求め、それを一つの抵抗とみなして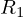 との直列回路として計算していきます。
との直列回路として計算していきます。
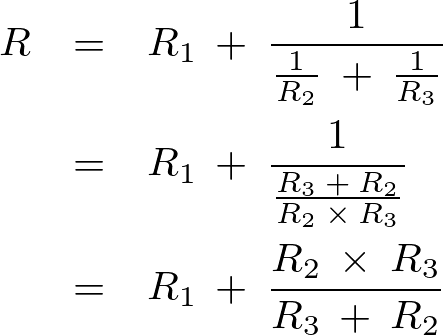
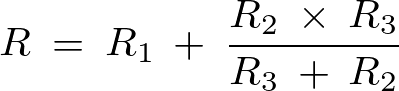
となるのでこれらに図にある通りに値を代入して計算していきます。
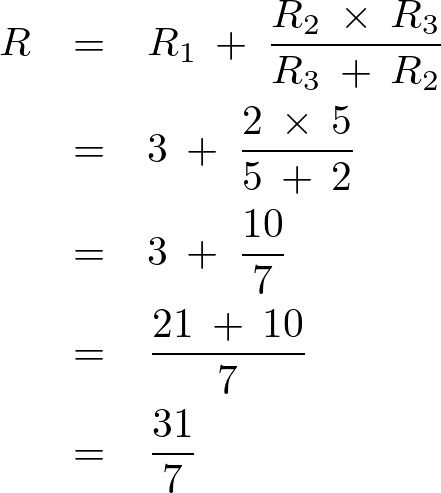
ゆえに以下のように求まります。
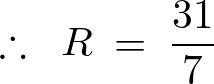
-
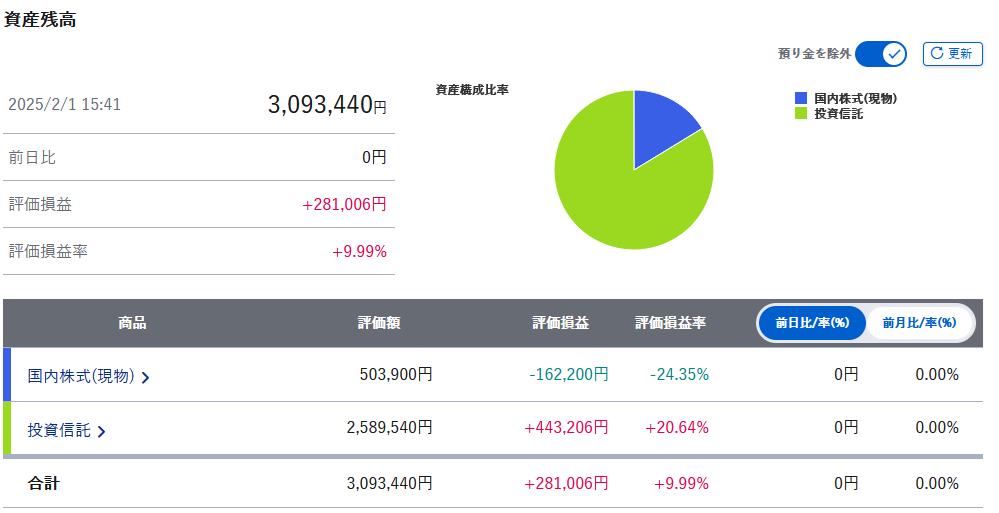
2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-
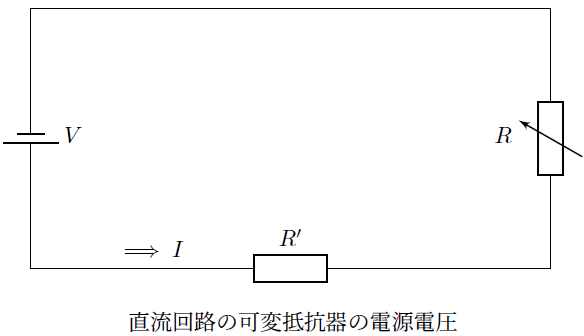
可変抵抗器の直列回路
続きを読む
-
Packet Tracer
続きを読む
-
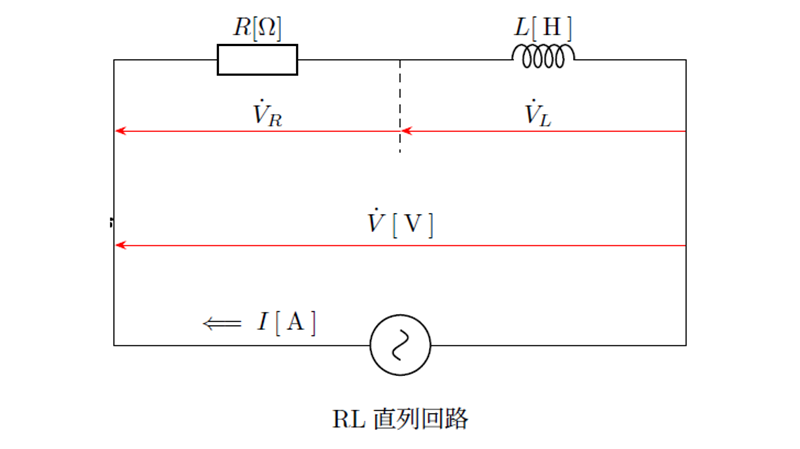
交流回路の直列接続
続きを読む
-
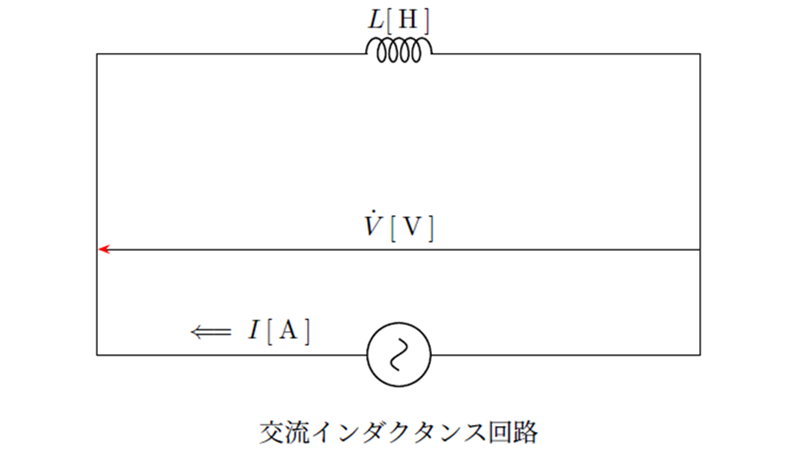
交流回路
続きを読む
テスト投稿
-

2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-

可変抵抗器の直列回路
続きを読む
-

Packet Tracer
続きを読む
-

交流回路の直列接続
続きを読む
-

交流回路
続きを読む