Rで重回帰分析-大気汚染①
重回帰分析とは
単回帰分析の説明変数がひとつなのに対して説明変数が2個以上あるデータモデルを考え、推定量が下のような多次元のベクトル分布、
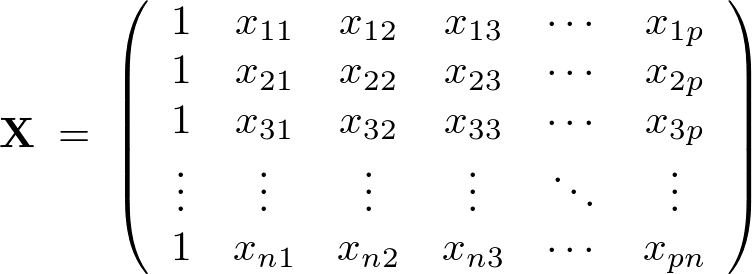
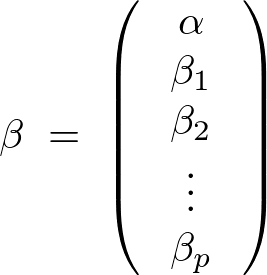

であるような説明変数、目的変数、回帰係数からなるデータ構造を考慮して次のようなデータモデルを考えます。
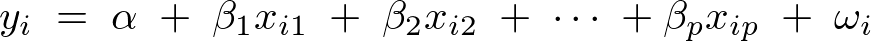
上記式の回帰直線における![]() は切片を表し、
は切片を表し、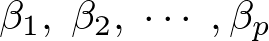 は回帰係数になります。
は回帰係数になります。
残差平方和という考え
切片である![]() と傾き
と傾き の回帰直線を予測した式
の回帰直線を予測した式 の式と実際の観測値
の式と実際の観測値 との差を残差として次のように考えることにします。
との差を残差として次のように考えることにします。
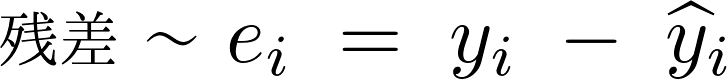
ハットは予測値や推定値を表す際に用いられるものになります。
そしてこれらの![]() 個の観測値に対する残差の二乗和~残差平方和を次のように表すことにします。
個の観測値に対する残差の二乗和~残差平方和を次のように表すことにします。

上記式において実際の観測値の差がなかった場合、つまり0であればこの残差平方和は0になると考え、この残差平方和が可能な限り0(最小)になるような回帰係数群を求める方法を最小2乗法(LSM:least squares method)と呼びます。
上記式においてそれぞれのパラメータであるα、βで偏微分しそれらを0と置いたものを採用していって正規方程式を導いていき、結果として次のような3つの式が求まります。
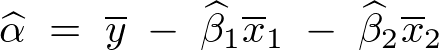
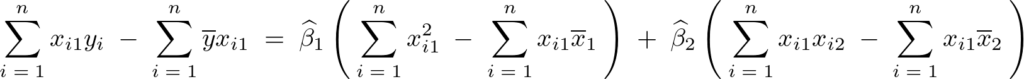
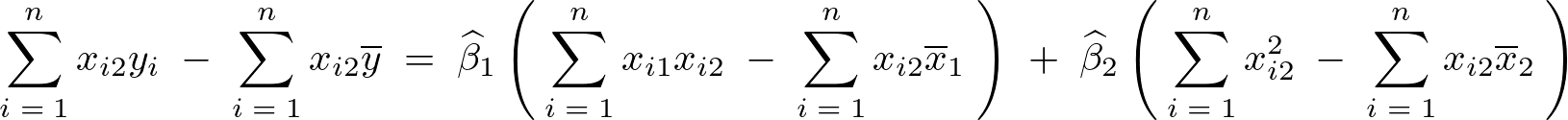
なお上記式の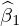 およおよび
およおよび に関しては不偏分散式などを変形して計算していけば次のようなものになります。
に関しては不偏分散式などを変形して計算していけば次のようなものになります。
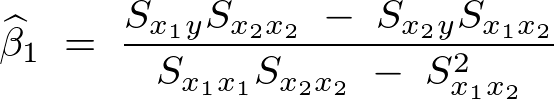
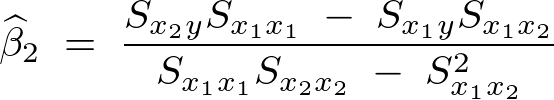
この一連の式の詳しい導出方法に関してはこちらのサイトをご参照ください。
またここより以下の書籍を参考に作成しています。
使用言語はRになります。
usair
大気汚染データ
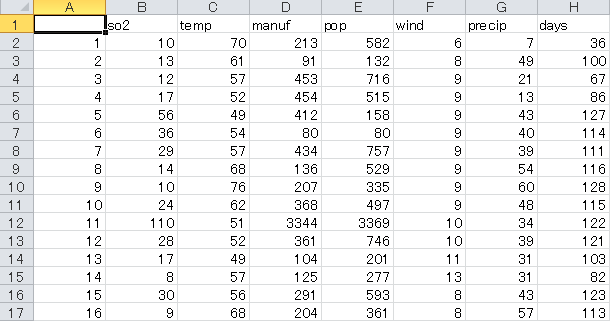
ダウンロードして開いたファイルには7つの変数名が書かれており7つあるそれぞれの変数の意味は次のようになります。
| SO2 | 大気中の1立方メートル当たりのSO2(二酸化硫黄)の量 |
| Temp | 年間平均気温 |
| Manuf | 20人以上の従業員を雇用している製造業の数 |
| Pop | 千人単位での人口数 |
| Wind | 時間当たりの年平均風速(マイル) |
| Precip | 年間の平均降水量(インチ) |
| Day | 年間の平均降水日数 |
得られたCSVファイルを読み込み次のようにしてデータを格納します。読み込む場合は2重引用符で囲むようにします。
usair_csv <- read.csv("usair.csv")
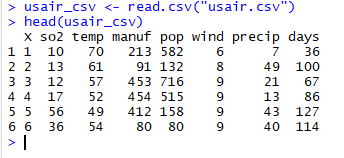
データの上部分の確認をするには次のように打ち込みます。
head(usair_csv)
ヒストグラムによるデータの可視化
histの後に()内でファイル名そのあと$で描画したい目的の変数を繋げます。
hist(usair_csv$so2)

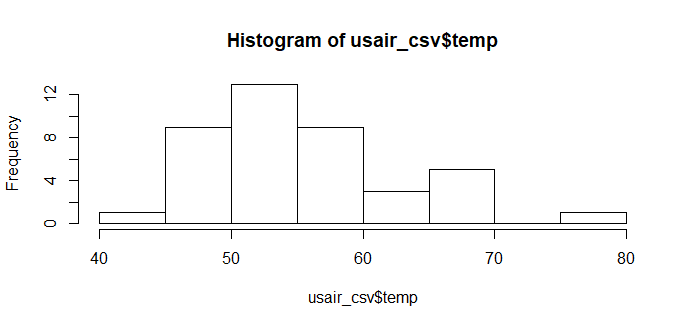
hist(usair_csv$temp)
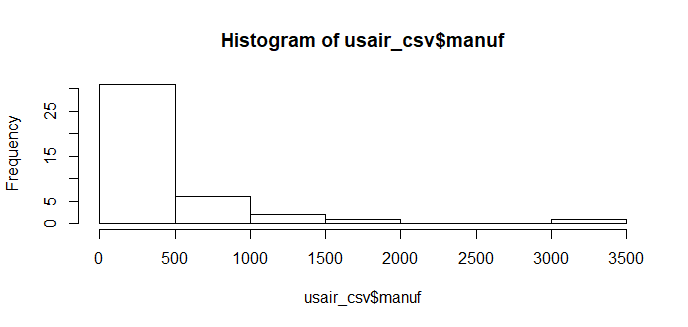
hist(usair_csv$manuf)
hist(usair_csv$pop)
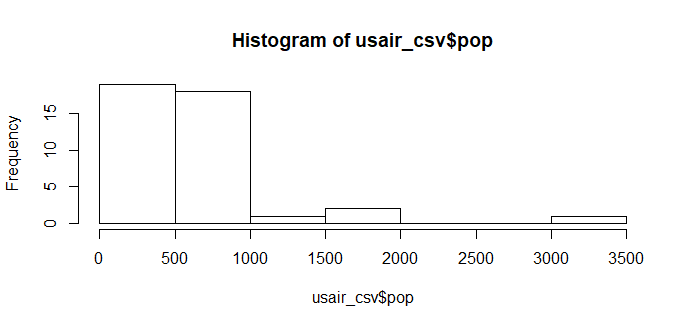
最初にデータを可視化することでデータの全体像を把握するのに役立ちます。
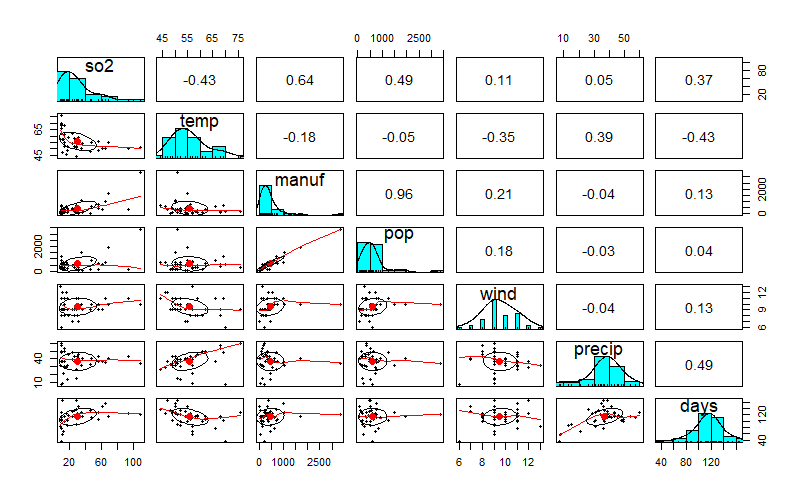
相関分析
目的変数とそれぞれの説明変数との関係性の大きさを見るために相関係数と散布図の出力を行います。
相関係数と散布図を同時に表示するpsychというパッケージを使ってデータを可視化します。
psychのインストール
install.packages("psych")
ライブラリ読み込み
library(psych)
usair_csv.fit <- usair_csv[,c(2,3,4,5,6,7,8)]
pairsで出力させます。
重回帰モデルの構築と要約
上の結果により目的変数のso2とその他変数の相関分析による関係性の強弱はわかりましたがひとまずすべての変数を使った重回帰分析と解析結果の要約を実行していきます。
so2を目的変数とし残りの変数を説明変数として重回帰モデルで説明していきます。 以下のように読み込ませ実行。
out_usair <- lm(so2 ~ temp + manuf + pop + wind + precip + days, data = usair_csv.fit)
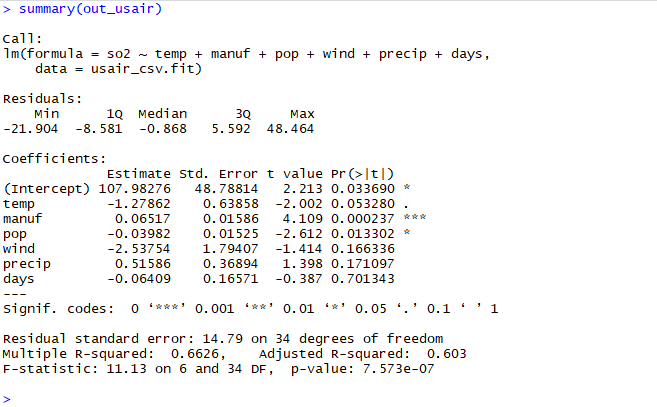
| 共変量 | 回帰係数の推定値 | 標準偏差 | t値 | p値 |
| Intercept | 107.98276 | 48.78814 | 2.213 | 0.033690 |
| temp | -1.27862 | 0.63858 | -2.002 | 0.053280 |
| manuf | 0.06517 | 0.01586 | 4.109 | 0.000237 |
| pop | -0.03982 | 0.01525 | -2.612 | 0.013302 |
| Wind | -2.53754 | 1.79407 | -1.414 | 0.166336 |
| precip | 0.51586 | 0.36894 | 1.398 | 0.171097 |
| days | -0.06409 | 0.16571 | -0.387 | 0.701343 |
上記の結果のcoefficientsの部分を見てみるとmanufとpopの2つが二酸化硫黄のレベルを予測するのに最も適しているのがわかります。
また右に*印がついているのもmanufとpopでp値が小さいほど右に*印がつき(最大で3つ)優位な説明変数だということがわかります。
-
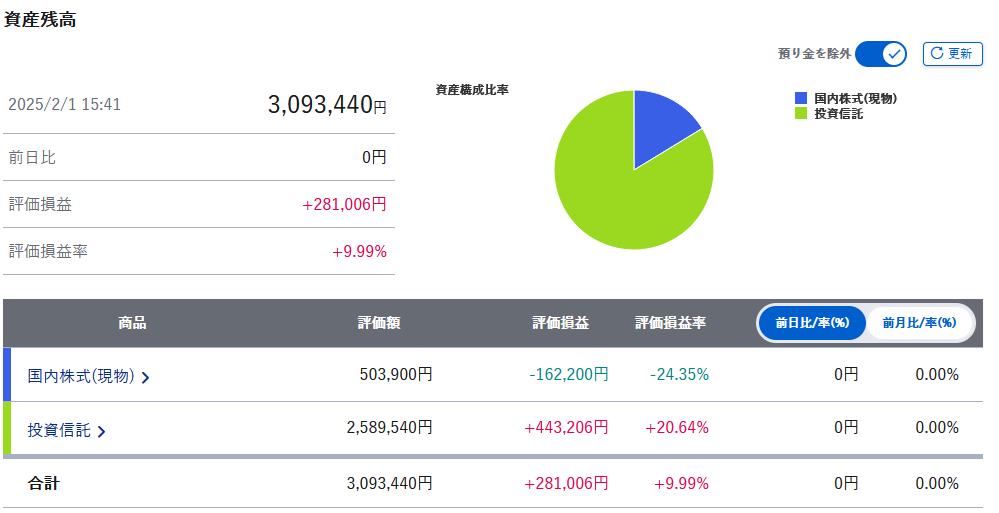
2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-
可変抵抗器の直列回路
続きを読む
-
Packet Tracer
続きを読む
-
交流回路の直列接続
続きを読む
-
交流回路
続きを読む
テスト投稿
-

2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-

可変抵抗器の直列回路
続きを読む
-

Packet Tracer
続きを読む
-

交流回路の直列接続
続きを読む
-

交流回路
続きを読む
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/35d429f6.6256710f.35d429f7.6ed9e8b0/?me_id=1275488&item_id=12653868&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbookoffonline%2Fcabinet%2F616%2F0016824951l.jpg%3F_ex%3D300x300&s=300x300&t=picttext)
