重回帰モデル
Rで重回帰分析 – 大気汚染②
目的とする変数の予測値を複数の説明変数の値によって予測しようとするモデルになります。
単回帰分析が一つ(一次元)の目的変数を一つの説明変数(一次元)によって推定する解析モデルになるのに対してこの重回帰分析モデルは単回帰モデルの説明変数が多次元になった複数のxのベクトルの形になっています。

目的変数の観測値を、

n個の説明変数、
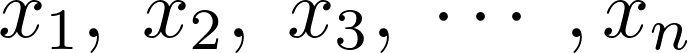
この観測値を以下のようにします。

目的変数が次のような多次元に展開されるようになります。
回帰係数を次のように置きます。

この回帰係数は説明変数が1単位分だけ変化した場合のそれぞれの目的変数の変化量を表しています。
切片を として推定量を次のような行列にします。
として推定量を次のような行列にします。
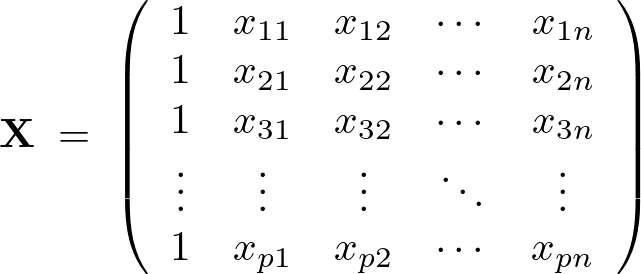
 を切片(intercept)として行列とベクトルを使って重回帰モデルを表現すると次のような形に表現できることになります。
を切片(intercept)として行列とベクトルを使って重回帰モデルを表現すると次のような形に表現できることになります。
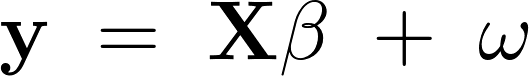
データの可視化
前回の内容から目的変数so2とした場合の相関関係が強いと思われるmanufとpopだけを使った相関分析を行ってみます。
usair_csv <- read.csv("usair.csv")
library(psych)
usair_csv.fit <- usair_csv[,c(2,4,5)]
psych::pairs.panels(usair_csv.fit)
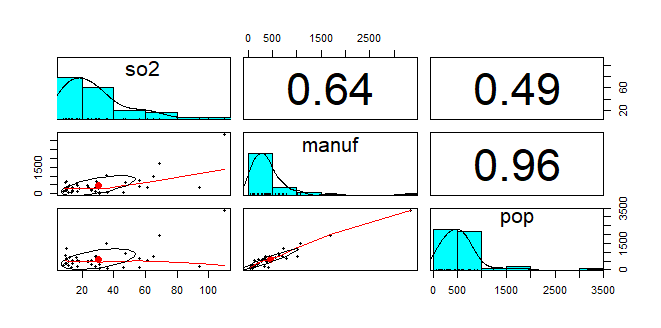
manufとpopの相関関係が強くそれぞれが目的変数であるso2のとの相関が高いことが見て取れます。
相関分析
out_usair <- lm(so2 ~ manuf + pop , data = usair_csv.fit)
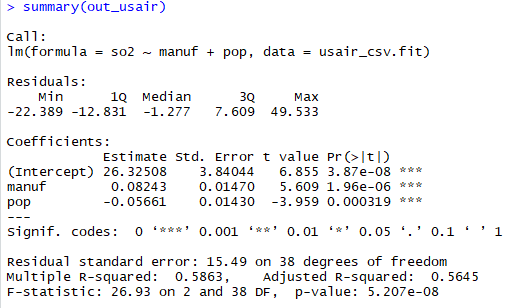
重回帰モデル要約のそれぞれの意味
| Estimete | 偏回帰係数の推定値 |
|---|---|
| Std.Error | 偏回帰係数の標準誤差 |
| t.value | t_0(偏回帰係数の推定値/標準誤差) |
| Pr(>|t|) | p値 |
これより結果は以下のようになります。
回帰係数の推定値
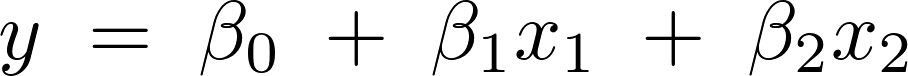
上記式において が切片、
が切片、 がmanuf、
がmanuf、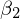 が人口になります。
が人口になります。
結果より切片が、

manufは、

さらにpopは、

これらにより次のように偏回帰係数が求まります。
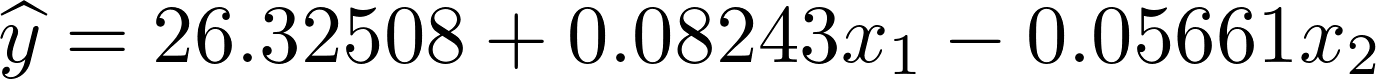
予測値
データを仮に工場数を500、人口の値を700などにしたそれぞれの変数を、

とした場合、上記式は次のように代入して予測値として繰り出せるようになります。
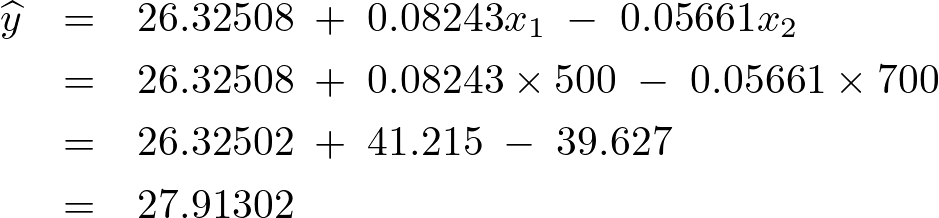
より次のような予測モデルが導かれます。

一つの偏回帰係数の値がほかの偏回帰係数を固定したままで対象となる偏回帰係数が増減した場合、目的変数の値がどの程度増減するのかを示しています。
例えば上記の式で言うとmanufの値が一つ増えた場合、以下、

であると仮定した場合、その予測値は、次のような計算式によって置き換えられることになります。
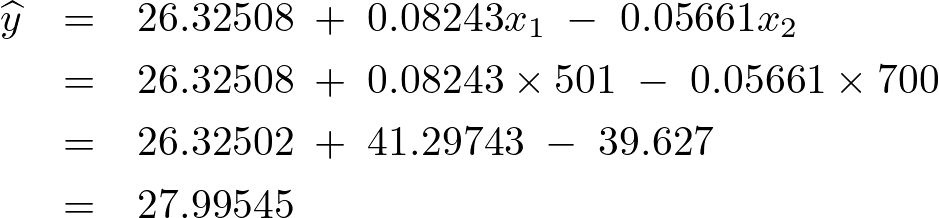
manufの値を1上げればso2の予測値は27.995454となり、その差分は以下のようになります。
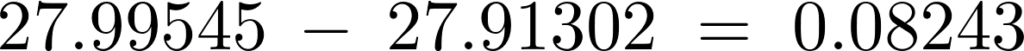
これは上記の式の例でいえば、manufの値が1上がればso2の予測値の値が0.08243ほど上昇するという予測がたてられることを意味しています。
-
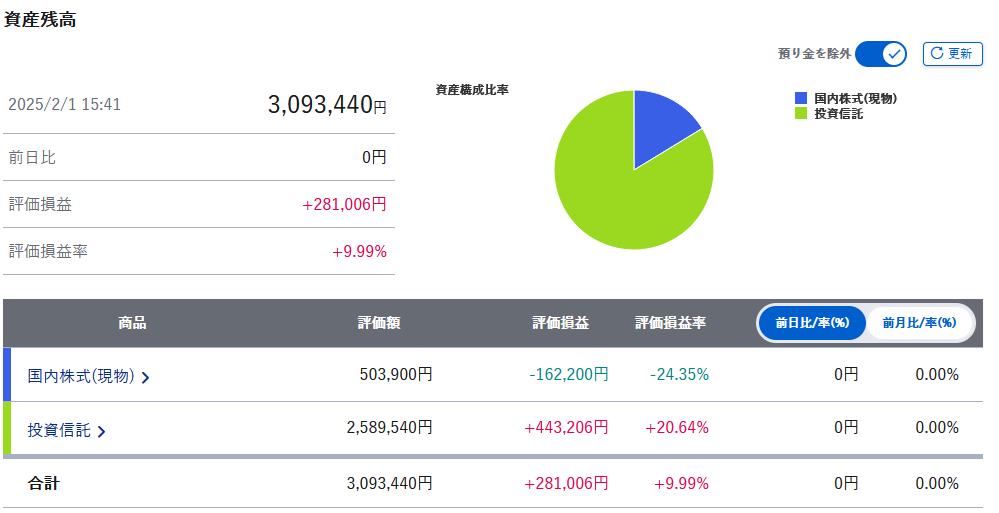
2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-
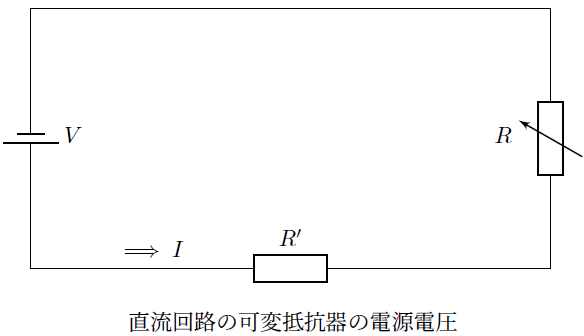
可変抵抗器の直列回路
続きを読む
-
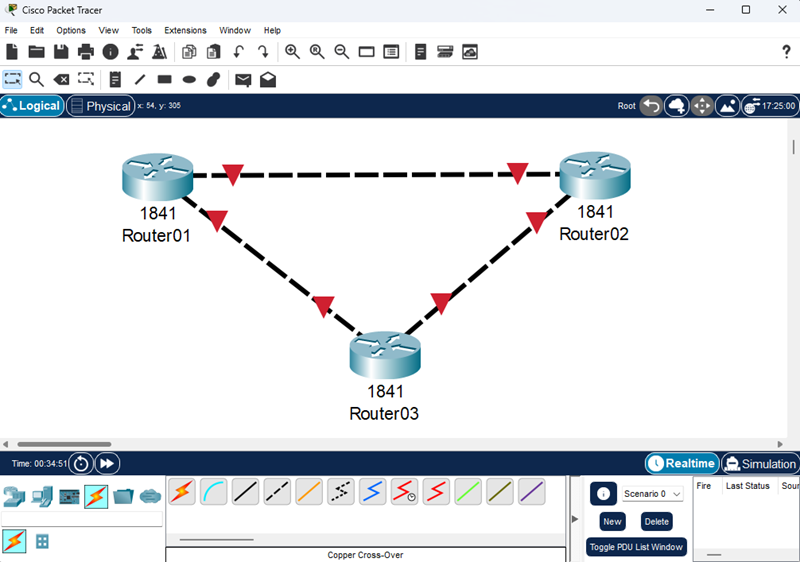
Packet Tracer
続きを読む
-
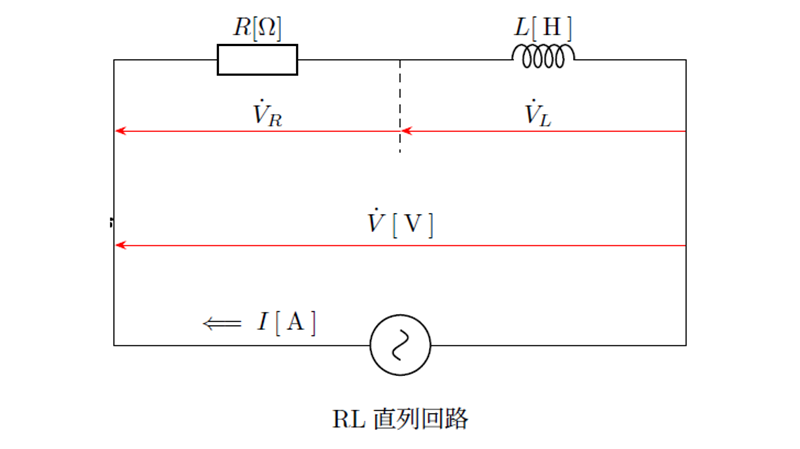
交流回路の直列接続
続きを読む
-
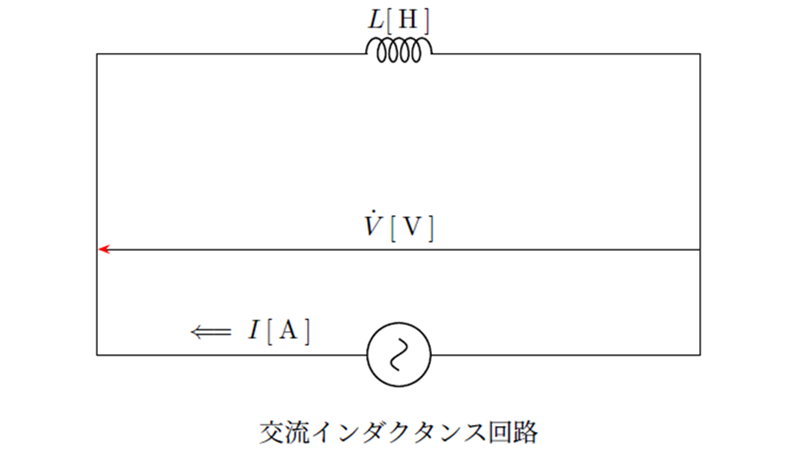
交流回路
続きを読む
テスト投稿
-

2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-

可変抵抗器の直列回路
続きを読む
-

Packet Tracer
続きを読む
-

交流回路の直列接続
続きを読む
-

交流回路
続きを読む