感染率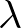 の違いによる
の違いによる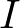 の比較
の比較
人口と感染症の数理モデルとしてのSIRモデルにて、感染率の違いによる感染者数の増減をグラフ化してどのようになるかをR Studioを使用して比較してみましょう。
感染率の違いによる感染者数の増減比較
感染率の違いによる感染者数の増減をグラフ化してどのよになるかを比較してみましょう。
感染率を0.9と0.4にした場合の比較で今回は変数S、I、Rをそれぞれ簡単にしてRを0とします。
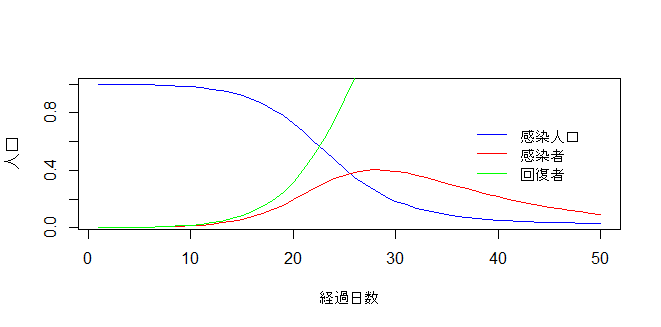
感染率90%の場合
次のように入力していきます。パッケージのodeをインストールしていない場合はインストールしておいてください。
sir2021_90 <- function(t, y, parameters){
with(
as.list(c(parameters, y)),
list(c
(S = -lambda * S * I,
I = lambda * S * I - gamma * I,
R = lambda * I)
)
)
}
R=0としてSはS = 0.999、Iは I = 0.001として値を代入していきます。
y_init <- c(S = 0.999, I = 0.001, R = 0)
感染率![]() 、
、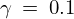 として入力していきます。
として入力していきます。
out2021_90 <- ode(y = y_init, times = 1:50, func = sir2021_90, parms = c(lambda = 0.9, gamma = 0.1))
write.csv(out2021_90, "out2021_90.csv")
out2021_90_csv <- read.csv("out2021_90.csv",header=TRUE,sep=",")
out2021_90_data <- read.csv(file = "out2021_90.csv", header = TRUE, sep = ",")
out2021_90_data_1 <- as.data.frame(out2021_90_data)
Withを使ってSIRそれぞれを描画するために以下のように入力していきます。
with(out2021_90_data_1, {
plot(time, S, type = "l", col = "blue", xlab = "経過日数", ylab = "人口")
lines(time, I, col = "red")
lines(time, R, col = "green")
})
legend("right", c("感染人口", "感染者", "回復者"), col = c("blue", "red", "green"), lty = 1, bty = "n")
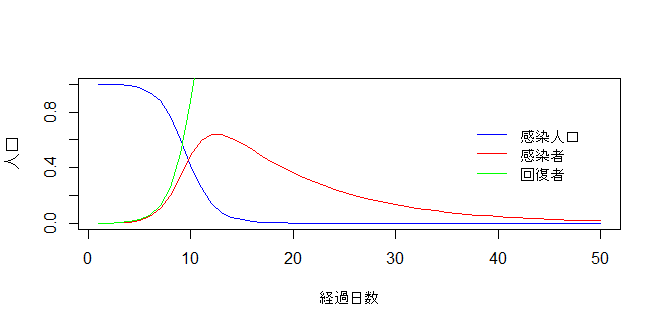
感染率40%の場合
sir2021_40 <- function(t, y, parameters){
with(
as.list(c(parameters, y)),
list(c
(S = -lambda * S * I,
I = lambda * S * I - gamma * I,
R = lambda * I)
)
)
}
y_init <- c(S = 0.999, I = 0.001, R = 0)
感染率を![]() 、
、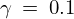 として入力していきます。
として入力していきます。
out2021_40 <- ode(y = y_init, times = 1:50, func = sir2021_40, parms = c(lambda = 0.4, gamma = 0.1))
write.csv(out2021_40, "out2021_40.csv")
out2021_40_csv <- read.csv("out2021_40.csv",header=TRUE,sep=",")
out2021_40_data <- read.csv(file = "out2021_40.csv", header = TRUE, sep = ",")
out2021_40_data_1 <- as.data.frame(out2021_40_data)
with(out2021_40_data_1, {
plot(time, S, type = "l", col = "blue", xlab = "経過日数", ylab = "人口")
lines(time, I, col = "red")
lines(time, R, col = "green")
})
legend("right", c("感染人口", "感染者", "回復者"), col = c("blue", "red", "green"), lty = 1, bty = "n")
2つの感染者数推移比較
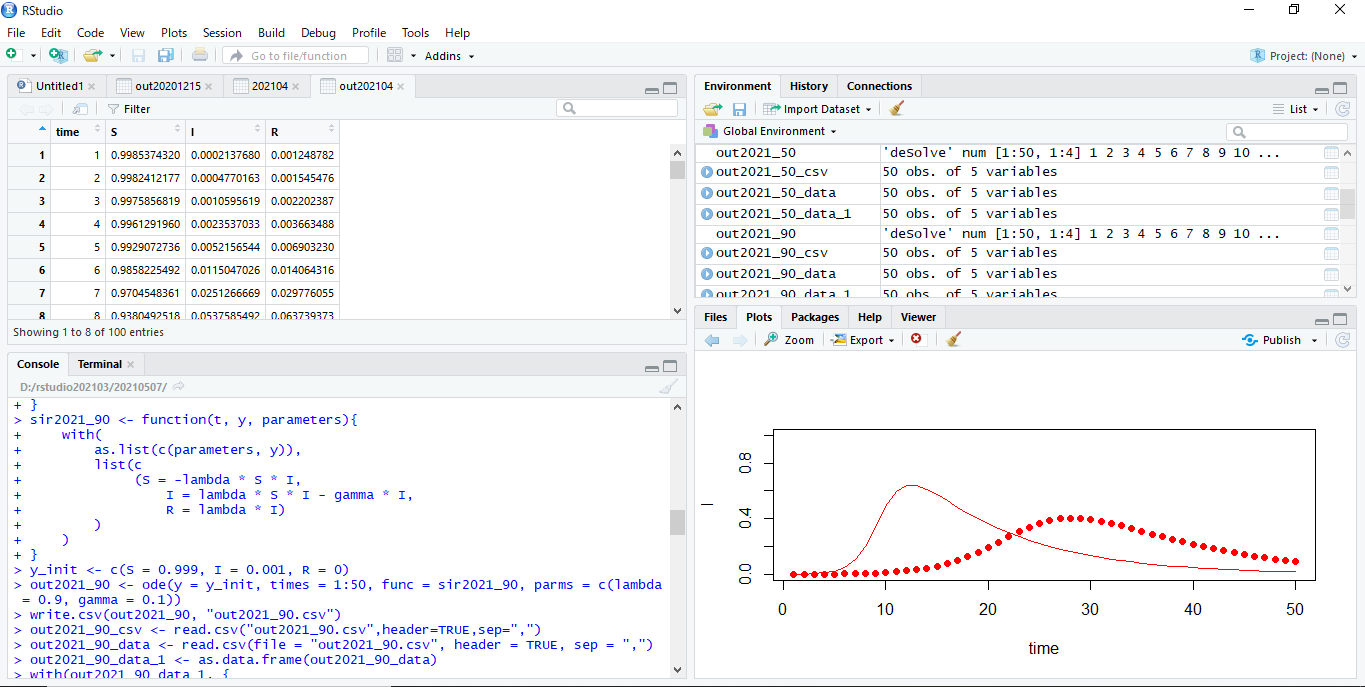
感染率40%の場合の感染者数の推移をグラフ化します。
with(out2021_40_data_1, plot(time, I, pch = 19, col = "red", ylim = c(0, 1)))
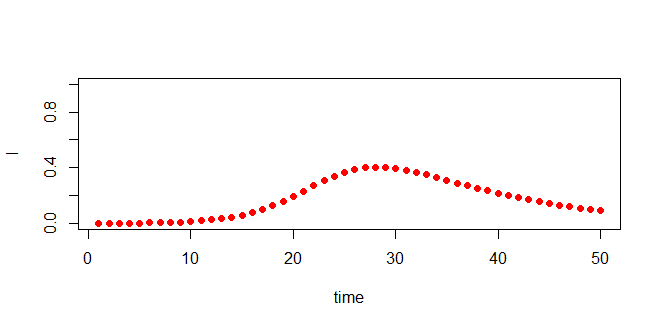
90%の場合に比べると山の形がなだらかで分散が大きいように見えます。
実際に上記のグラフと感染率90%のグラフとを比較してみましょう。
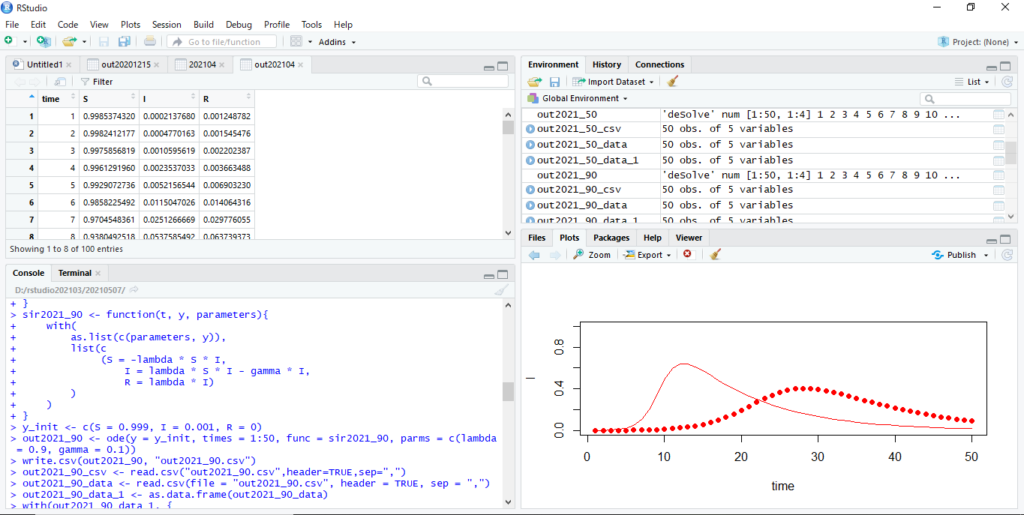
with(out2021_50_data_1, plot(time, I, pch = 19, col = "red", ylim = c(0, 1))) with(out2021_90_data_1, lines(time, I, col = "red"))
次のように出力されます。
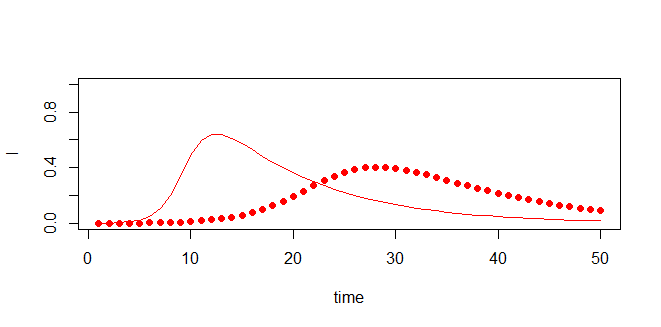
感染力を比較的抑えることができると上のプロット図のように一日当たりの感染者数を抑えられるようになります。
感染力抑止によって感染者流向のピークを下げさせて感染者数の増加の速さを抑制し感染拡大を抑止することができるということがわかります。
-
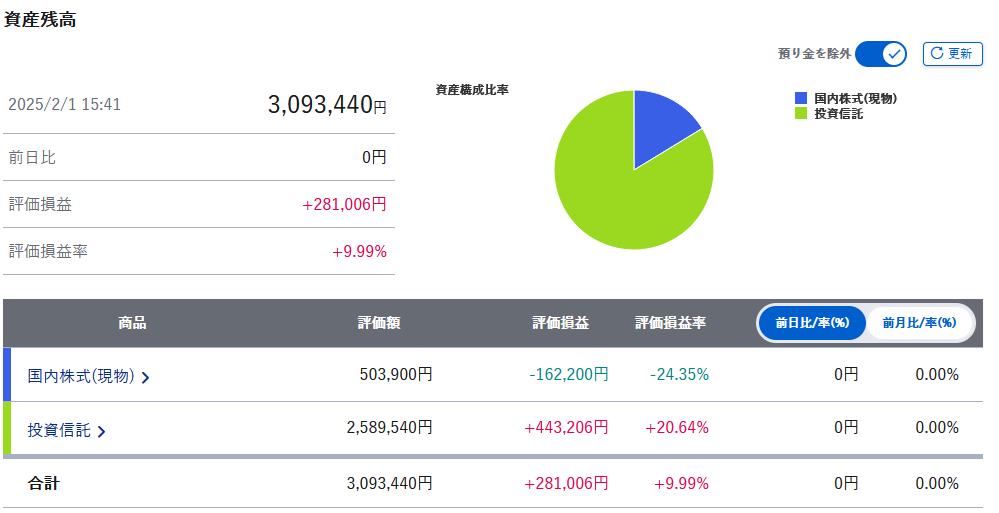
2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-
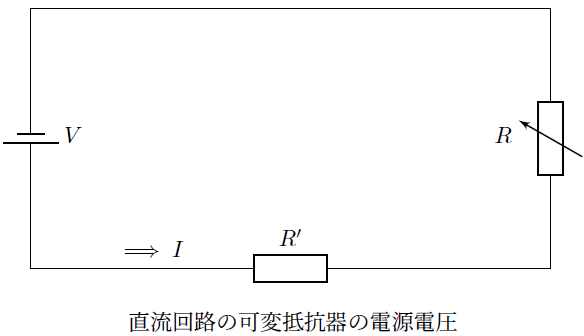
可変抵抗器の直列回路
続きを読む
-
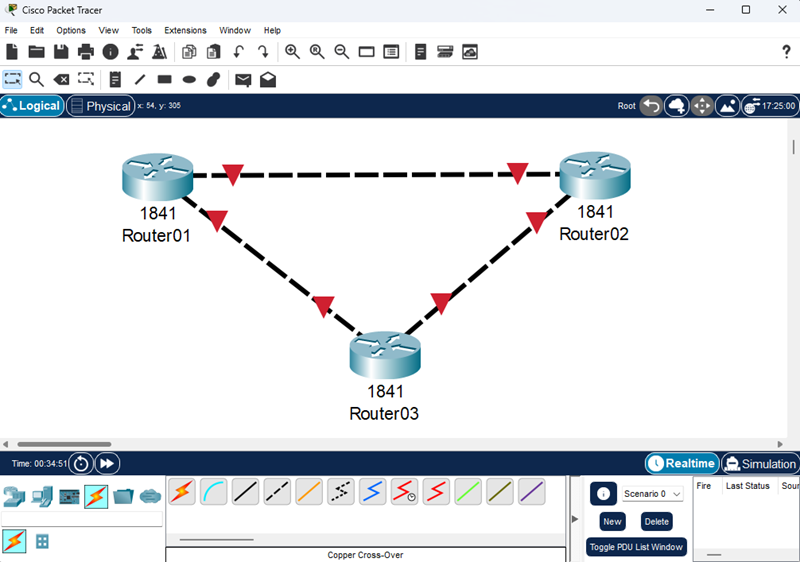
Packet Tracer
続きを読む
-
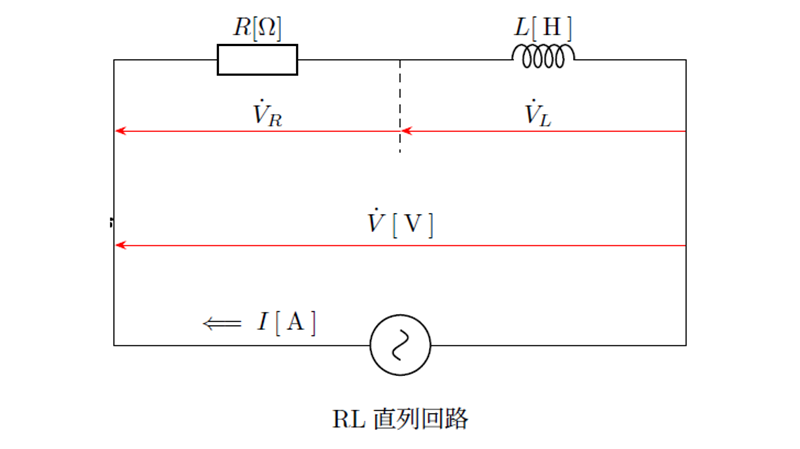
交流回路の直列接続
続きを読む
-
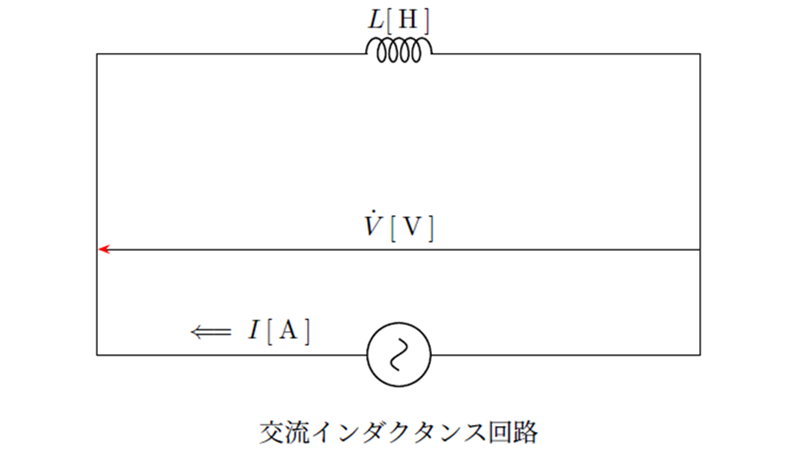
交流回路
続きを読む
テスト投稿
-

2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-

可変抵抗器の直列回路
続きを読む
-

Packet Tracer
続きを読む
-

交流回路の直列接続
続きを読む
-

交流回路
続きを読む