RstudioでSIRモデル②
RstudioでSIRモデル②
ケルマックマッケンドリック微分方程式
ケルマックマッケンドリック微分方程式(Kellogg-McKendrick differential equation)とは、人口動態や疫学において使われる微分方程式であり、この微分方程式は特定の条件下における人口動態をモデル化するために使用されるものになります。以下の3つの常微分方程式よりなります。
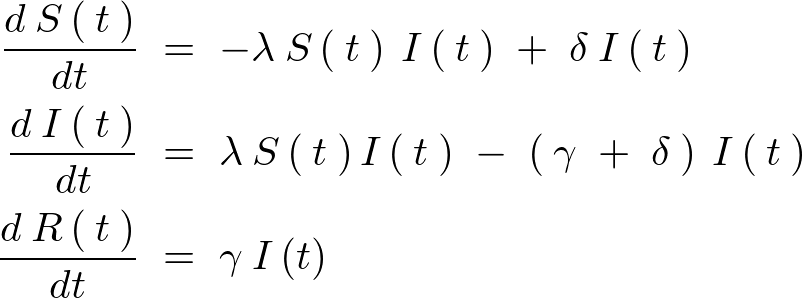
上記微分方程式において免疫力を獲得しないで回復する率![]() を
を![]() とおいた場合次のような関係式が関係式が求まります。
とおいた場合次のような関係式が関係式が求まります。
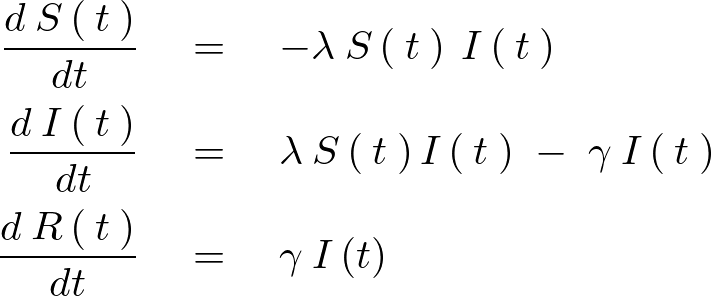
この上記式におけるそれぞれの集団が感染症に対して「感受性(Susceptible)」、「感染している(Infected)」、「回復(Recovered)」の3つの状態に分類されます。
また人口を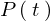 とすれば次のような関係式が成り立ちます。
とすれば次のような関係式が成り立ちます。
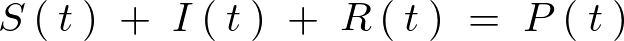
SIRモデル第2式に対する数理的考察
上記SIR式モデルにおける次の第2式、
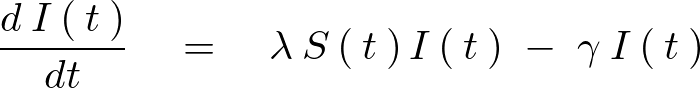
この微分方程式を解いていきます。
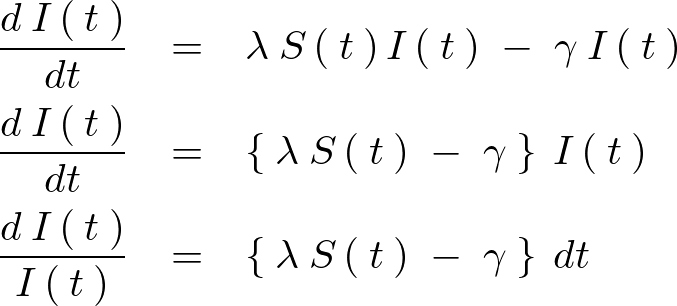
両辺に対して積分を実行します。
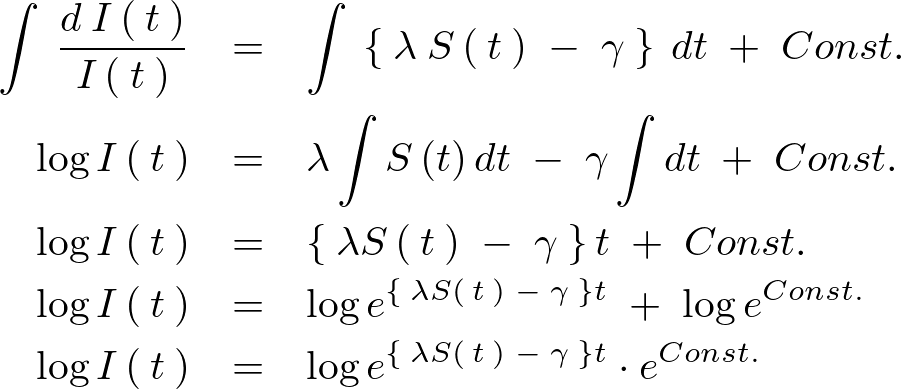
ここで以下のようにおきます。
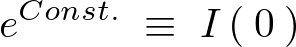
そうすると結果として以下のような式が求まります。
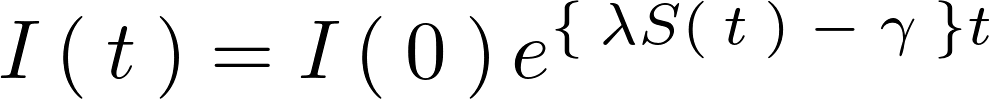
ここから次のようにしてイクスポーネンシャルの乗数部分に関して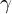 でくくって変形していきます。
でくくって変形していきます。
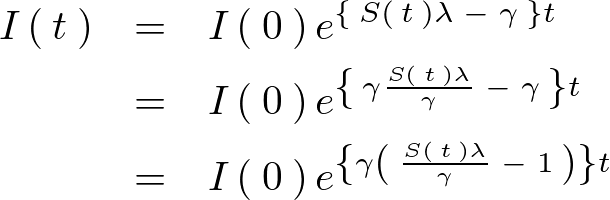
さらにここで上記乗数部分の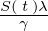 に関してそれを基本再生産数
に関してそれを基本再生産数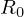 として次のようにおきます。
として次のようにおきます。
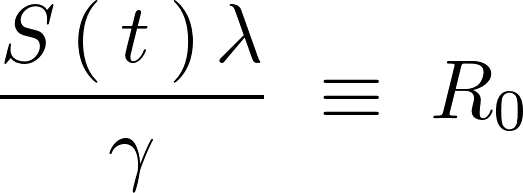
一般的に上記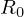 は
は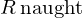 (Rノート)と呼ばれており、これを使えば先ほどの式は次のように表されることになります。
(Rノート)と呼ばれており、これを使えば先ほどの式は次のように表されることになります。
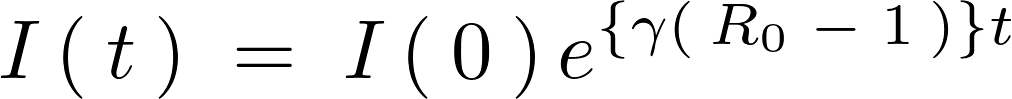
この結果によりイクスポーネンシャルの乗数部分が1以上であれば指数関数的に上昇していき、1以下であるならば収束するということがわかります。
R StudioでのSIRモデル計算
R studioを起動させ次のように打ち込みます。
sir202104 <- function(t, y, parameters){
with(
as.list(c(parameters, y)),
list(c
(S = -lambda * S * I,
I = lambda * S * I - gamma * I,
R = lambda * I)
)
)
}
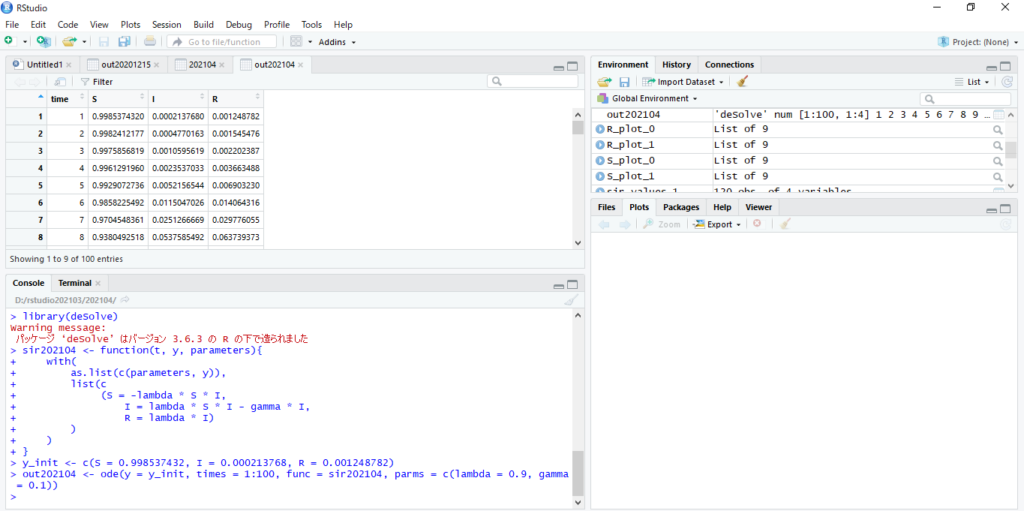
S、I、Rのそれぞれの変数に値を代入していきます。
ちなみに代入している値はあくまで架空の数値なので本気にしないようにしてください。
y_init <- c(S = 0.998537432, I = 0.000213768, R = 0.001248782)
out202104にy_init、経過日数の範囲、生成データ、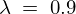 、
、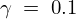 をdeSolveのパッケージ、“ode”を使って代入します。
をdeSolveのパッケージ、“ode”を使って代入します。
このodeが入っていないと動作しないのでライブラリ読み込みしていない場合はlibrary(deSolve)と打ち込んで読み込んでから出力をします。
out202104 <- ode(y = y_init, times = 1:100, func = sir202104, parms = c(lambda = 0.9, gamma = 0.1))
out202104を出力させます。
out202104 time S I R 1 1 0.9985374320 0.0002137680 0.001248782 2 2 0.9982412177 0.0004770163 0.001545476 3 3 0.9975856819 0.0010595619 0.002202387 4 4 0.9961291960 0.0023537033 0.003663488 5 5 0.9929072736 0.0052156544 0.006903230 6 6 0.9858225492 0.0115047026 0.014064316 7 7 0.9704548361 0.0251266669 0.029776055 8 8 0.9380492518 0.0537585492 0.063739373 9 9 0.8736448587 0.1102596172 0.134869298 10 10 0.7594138407 0.2089210159 0.274995872 11 11 0.5922624058 0.3484511232 0.523587821 12 12 0.4048325562 0.4936057964 0.904064409 13 13 0.2467751147 0.5966631001 1.399065649 ・・・(中略)・・・ 89 89 0.0001253295 0.0004536435 8.984798825 90 90 0.0001252808 0.0004105198 8.985187377 91 91 0.0001252368 0.0003714954 8.985538992 92 92 0.0001251969 0.0003361808 8.985857183 93 93 0.0001251609 0.0003042231 8.986145126 94 94 0.0001251283 0.0002753034 8.986405697 95 95 0.0001250988 0.0002491328 8.986641498 96 96 0.0001250721 0.0002254500 8.986854883 97 97 0.0001250479 0.0002040185 8.987047984 98 98 0.0001250261 0.0001846243 8.987222729 99 99 0.0001250063 0.0001670737 8.987380862 100 100 0.0001249884 0.0001511917 8.987523961
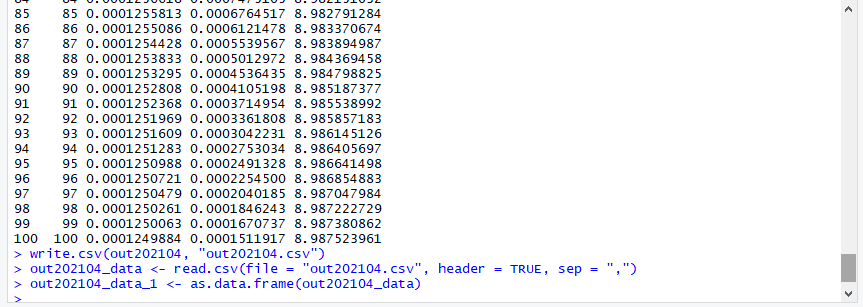
得られたデータのCSVへの格納
得られたデータをCSVファイルにします。
write.csv(out202104, "out202104.csv")
csvファイルの読み込み
csvファイルはカレントディレクトリに生成されても読み込みを行わないと認識されません。
次のように入力してEnterを押下します。
out202104_csv <- read.csv("out202104.csv",header=TRUE,sep=",")
これで読み込みができるようになります。
次のように入力してEnterを押せばデータが表示されます。
out202104_csv
X time S I R
1 1 1 0.9985374320 0.0002137680 0.001248782
2 2 2 0.9982412177 0.0004770163 0.001545476
3 3 3 0.9975856819 0.0010595619 0.002202387
・・・(中略)・・・
99 99 99 0.0001250063 0.0001670737 8.987380862
100 100 100 0.0001249884 0.0001511917 8.987523961
生成されたCSVファイルのデータをout202104_dataに格納します。
out202104_data <- read.csv(file = "out202104.csv", header = TRUE, sep = ",")
out2021004_data_1にデータフレームを格納します。
out202104_data_1 <- as.data.frame(out202104_data)
3つのグラフを同時に描画
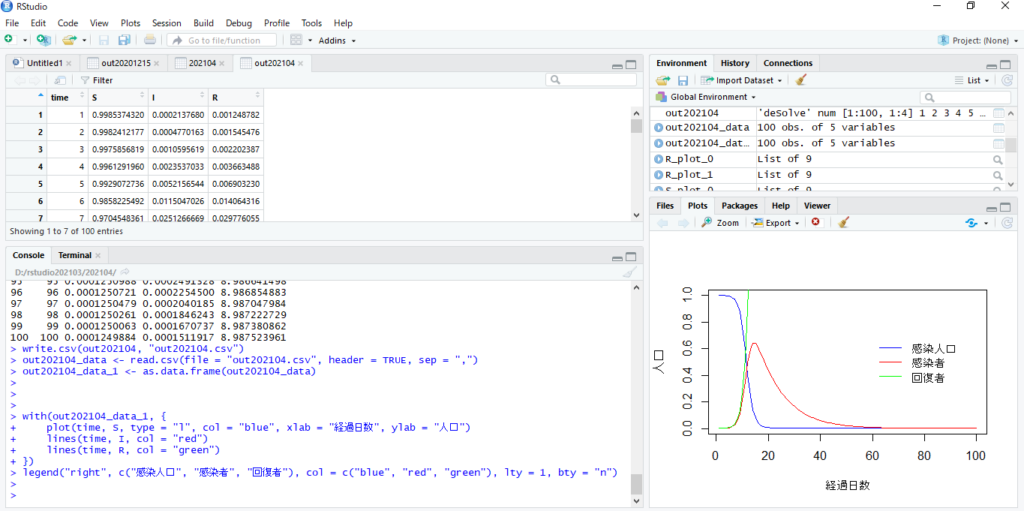
withを使ってSIRを描画。次のように入力します。
with(out202104_data_1, {
plot(time, S, type = "l", col = "blue", xlab = "経過日数", ylab = "人口")
lines(time, I, col = "red")
lines(time, R, col = "green")
})
legend("right", c("感染人口", "感染者", "回復者"), col = c("blue", "red", "green"), lty = 1, bty = "n")
上記のように打ち込んでEnterを押せば以下のように画像が出力されます。
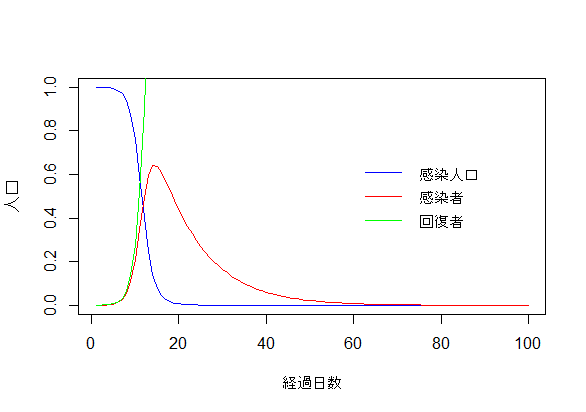
-
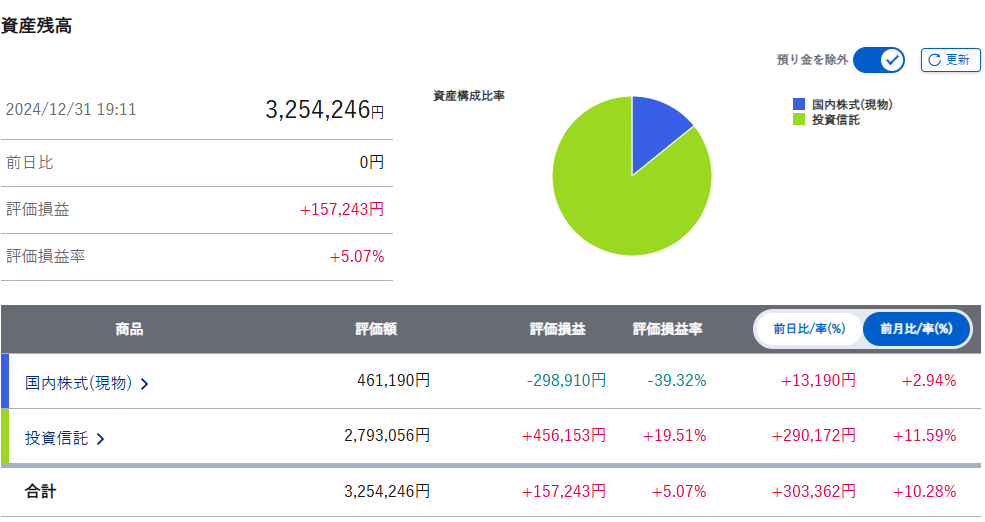
2024年12月NISA運用概況
続きを読む
-

2024年12月金運用成績
続きを読む
-
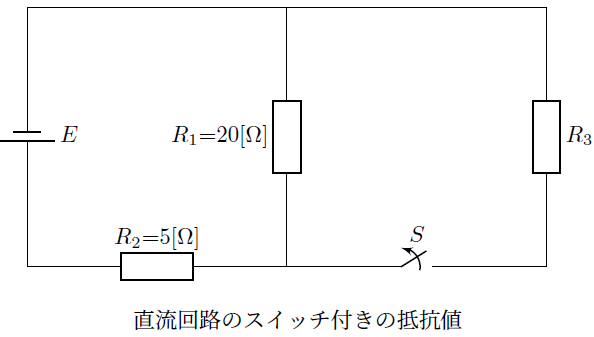
スイッチ付き回路素子の抵抗値
続きを読む
-
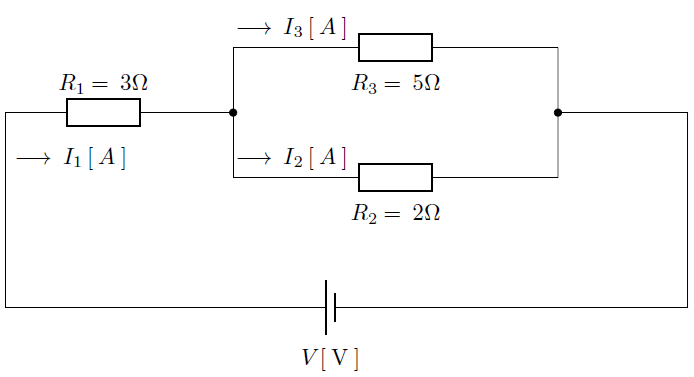
直流回路の合成抵抗
続きを読む
-
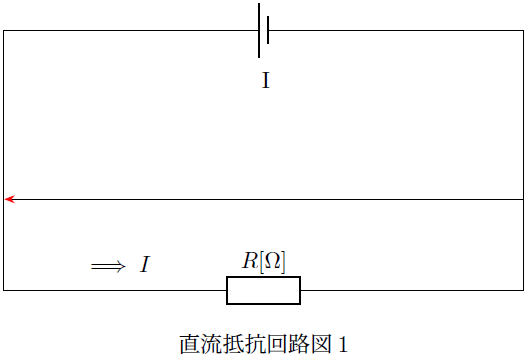
直流回路
続きを読む
-
電気数学理論
続きを読む
テスト投稿
-

2024年12月NISA運用概況
続きを読む
-

2024年12月金運用成績
続きを読む
-

スイッチ付き回路素子の抵抗値
続きを読む
-

直流回路の合成抵抗
続きを読む
-

直流回路
続きを読む
-

電気数学理論
続きを読む