テイラー展開
テイラー展開~関数の近似
多項式の展開
例えば次のような式、
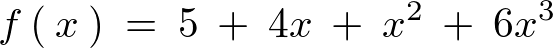
この式を、
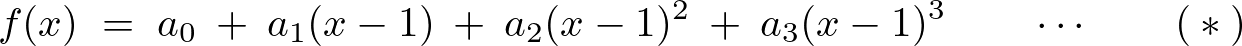
といった形にすることを考えてみます。 まず、式を次々に微分していくと、
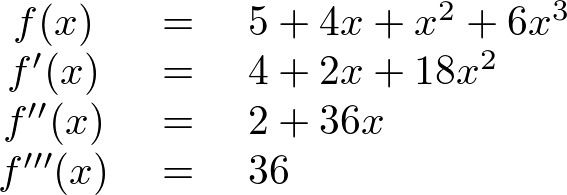
ここで![]() に1を代入していくと、
に1を代入していくと、
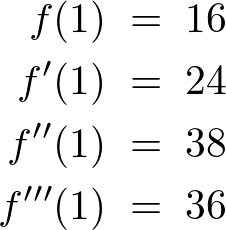
という結果が出てきますが、ここで の式を
の式を![]() とおくと、まず、
とおくと、まず、
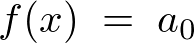
次に、![]() を求めるために
を求めるために の式をxで微分し、1を代入すると、
の式をxで微分し、1を代入すると、
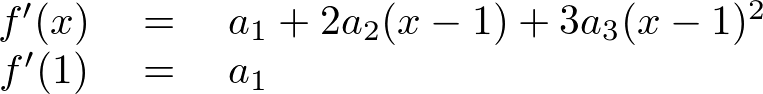
であることがわかります。
なお、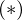 の式の微分は合成関数微分を使っています。
の式の微分は合成関数微分を使っています。
例えば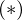 の第3項は次のように微分を行っています。
の第3項は次のように微分を行っています。
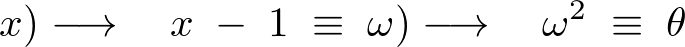
より、
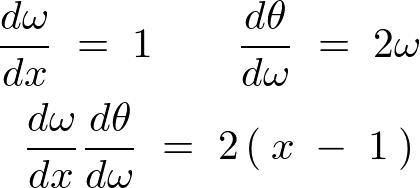
として計算しています。
さらに微分して同じように1を代入すれば、
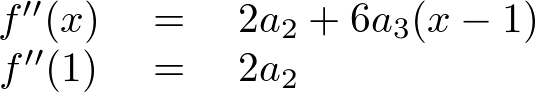
同様に、
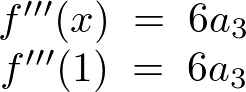
ここで注目すべきことは上記の結果を勘案すると次のような関係があるということです。
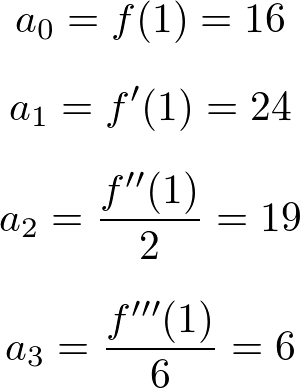
以上の結果を用いれば、 の式は次のような形で表すことができるようになります。
の式は次のような形で表すことができるようになります。
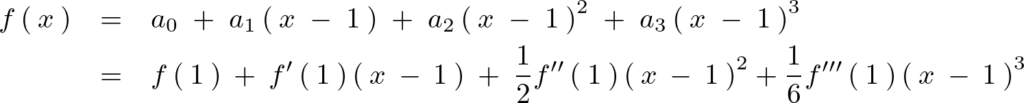
ここまでは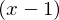 についての多項式展開をしてきましたがそれ以外の
についての多項式展開をしてきましたがそれ以外の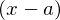 についてもまた同様になります。
についてもまた同様になります。
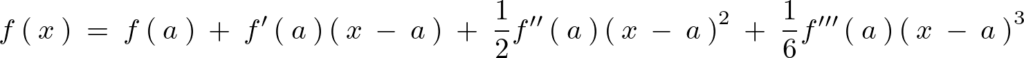
上記の式は3次の多項式ならば成立する式であり、
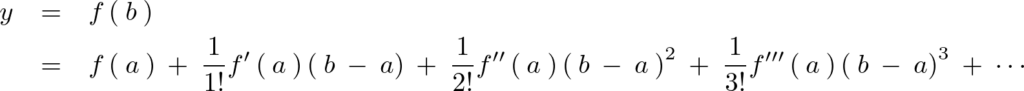
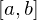 を含む開区間で
を含む開区間で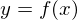 が微分可能なとき次のようなことが言えます。
が微分可能なとき次のようなことが言えます。
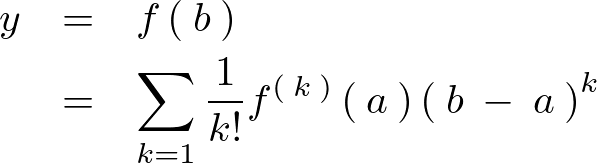
以上をテイラー展開と呼び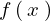 式の
式の![]() での値を
での値を![]() まわりで展開するといったりします。
まわりで展開するといったりします。
ちなみに分母にある![]() というのは、kのカイジョウとよび、以下のように定義されているものです。
というのは、kのカイジョウとよび、以下のように定義されているものです。
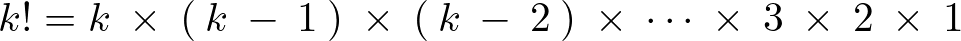
例えば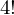 だった場合、
だった場合、
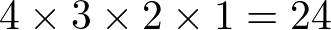
となります。ちなみに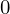 のカイジョウは
のカイジョウは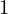 になります。
になります。
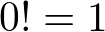
上記のやり方に手をくわえたもので![]() 点回りにおけるテイラー級数があります。これは一般的にマクローリン展開などと呼ばれています。
点回りにおけるテイラー級数があります。これは一般的にマクローリン展開などと呼ばれています。
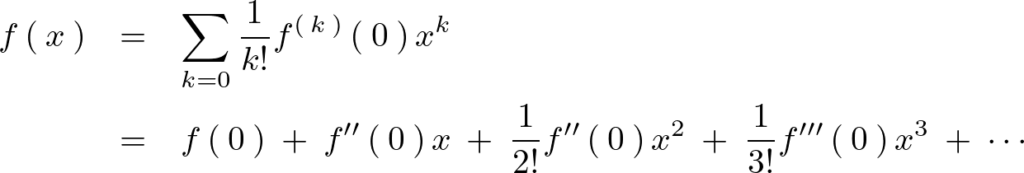
例題
次に示す関数を![]() まわりでテイラー展開(マクローリン展開)してみましょう。
まわりでテイラー展開(マクローリン展開)してみましょう。

答え
(1)
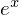 は
は![]() でいくら微分していっても同じ結果が出てくるので0点まわりのテイラー展開、
でいくら微分していっても同じ結果が出てくるので0点まわりのテイラー展開、
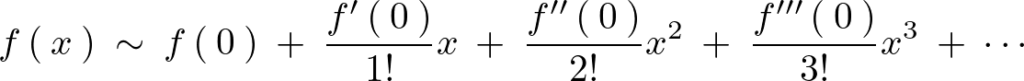
にあてはめれば次のようになります。
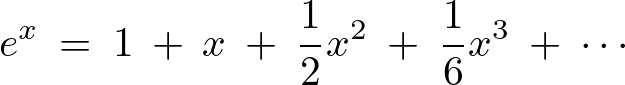
(2)
合成関数の微分を施します。
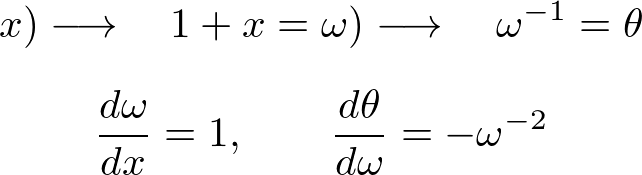
などとやって3階微分までやっていくと、
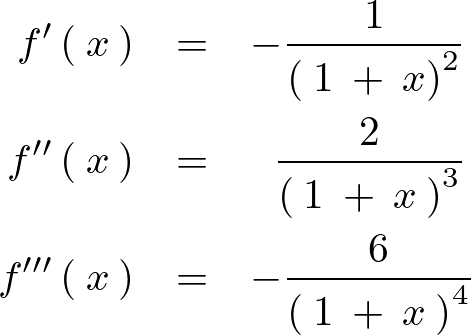
のようになります。これを代入していけば、
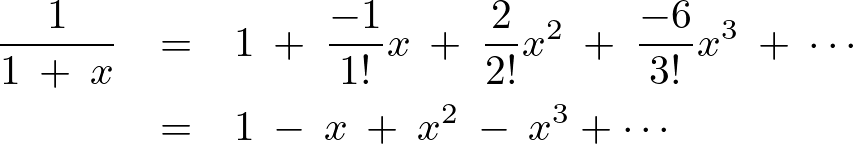
設問の例
問題の中にはテイラー展開せよ、と明確に表現することなく次のような感じで出題されることもあります。
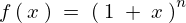 といった式があった場合、この関数
といった式があった場合、この関数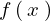 を第3項までのべき級数展開して表示せよ、などという設問があった場合はたいていは次のようにマクローリン展開して問題を解いていきます。
を第3項までのべき級数展開して表示せよ、などという設問があった場合はたいていは次のようにマクローリン展開して問題を解いていきます。
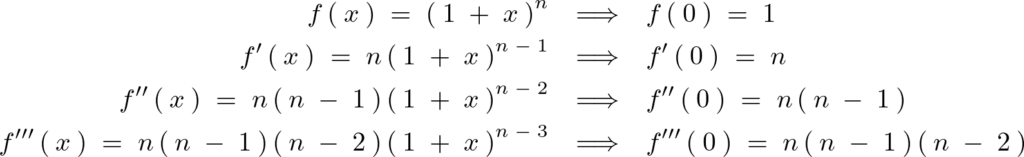
よって解答としては以下のようになります。
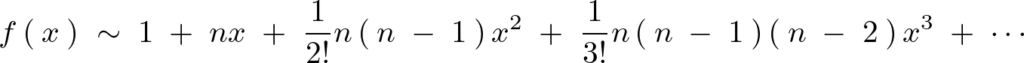
補遺
すべての級数がテイラー展開でうまくいくとは限りません。
例えば次のような式を級数展開する場合はテイラー展開をするとごちゃごちゃした式が出てくるので別の方法を使います。

まず、
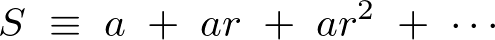
のような級数を考えて、それにさらに定数項の![]() を両辺に加えたものを用いて次のような式を導きます。
を両辺に加えたものを用いて次のような式を導きます。
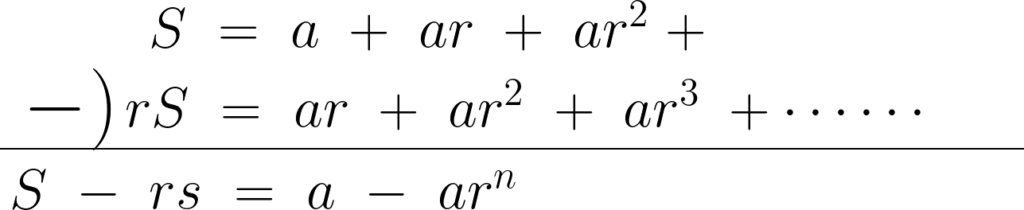

ここで![]() を
を![]() として仮定すれば、
として仮定すれば、
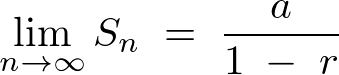
に当てはめて![]() とおいて上式に当てはめていけば、
とおいて上式に当てはめていけば、
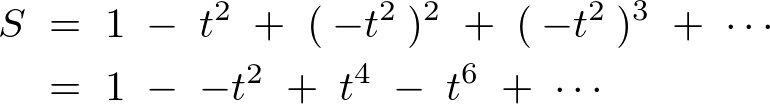
ここでこの式の両辺を0から1の定積分を実行します。まず右辺は、
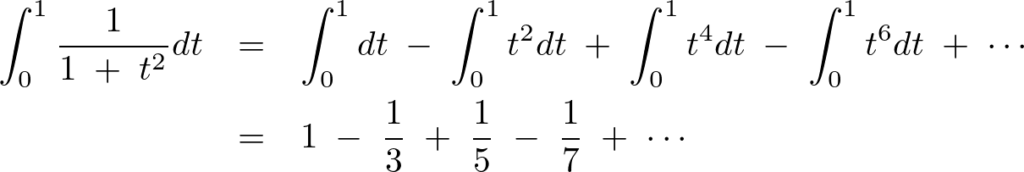
一方、左辺の積分に関して、テイラー展開の微分は、
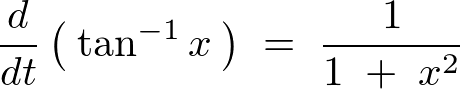
であったので0から1までの定積分を行うと、
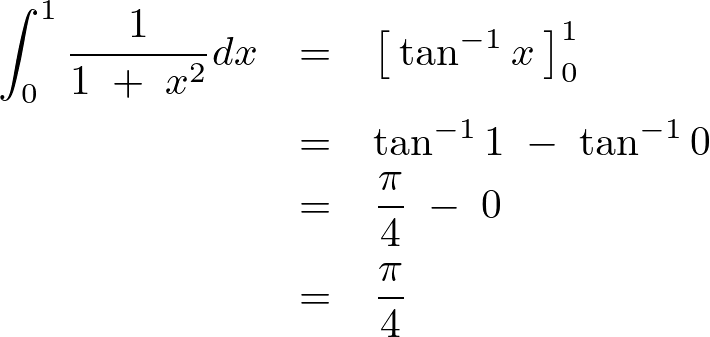
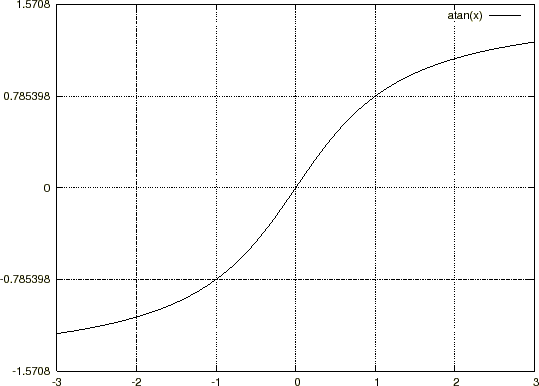
ここで左図アークタンジェントのグラフより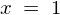 のところで交わる
のところで交わる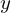 軸の値の0.785…と言う数字は3.14…を4で割った数、すなわち
軸の値の0.785…と言う数字は3.14…を4で割った数、すなわち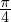 になります。
になります。
となるので次のような関係式が導かれます。
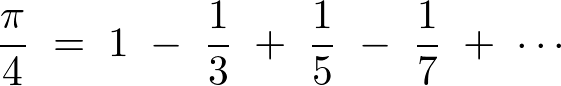
この式は結構有名な数式らしく、数学の読み物的なテキストなんかではたまに紹介されることもあるようです。 一般的にはグレゴリーの公式、またはライプニッツの公式などといわれているらしいです。
-
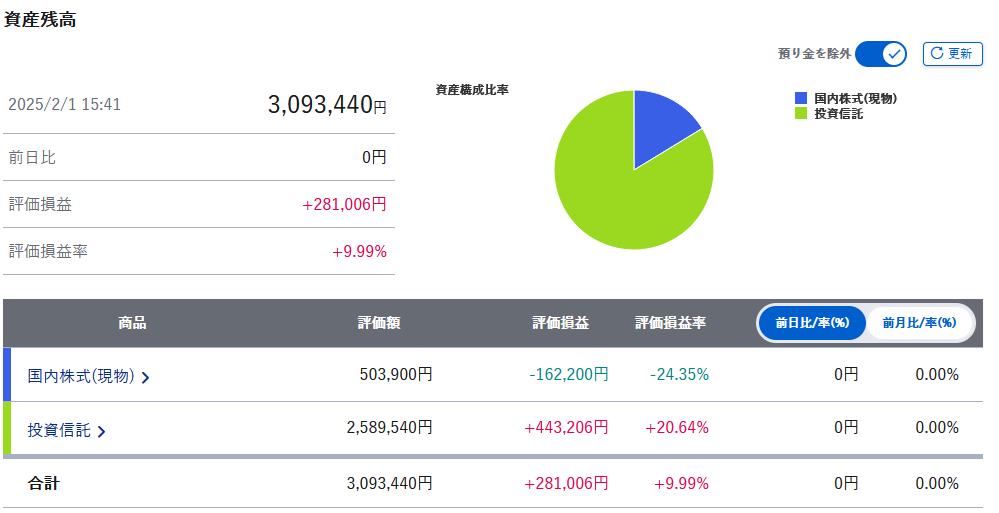
2025年1月NISA運用概況
カテゴリー
-

2025年1月金運用概況
カテゴリー
-
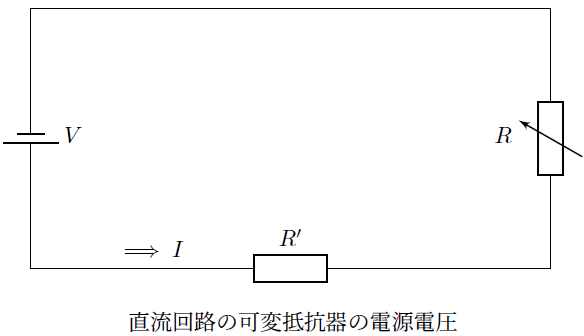
可変抵抗器の直列回路
カテゴリー
-
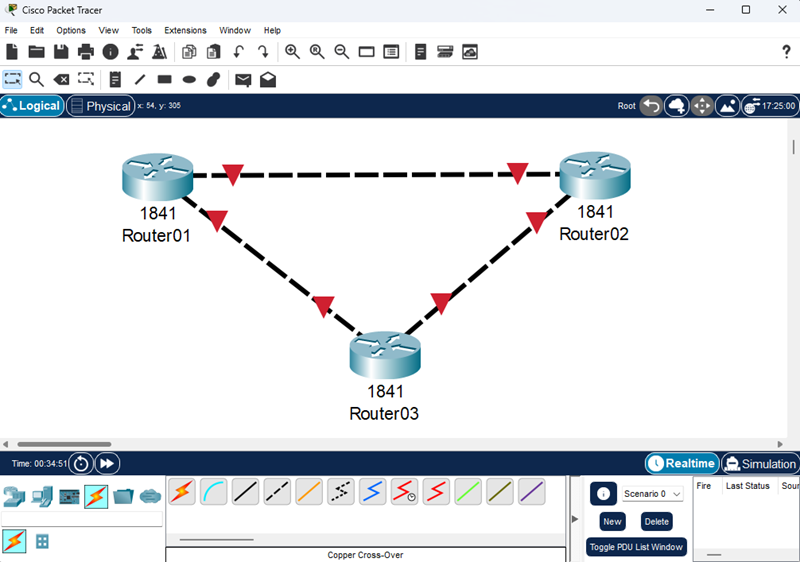
Packet Tracer
カテゴリー
-
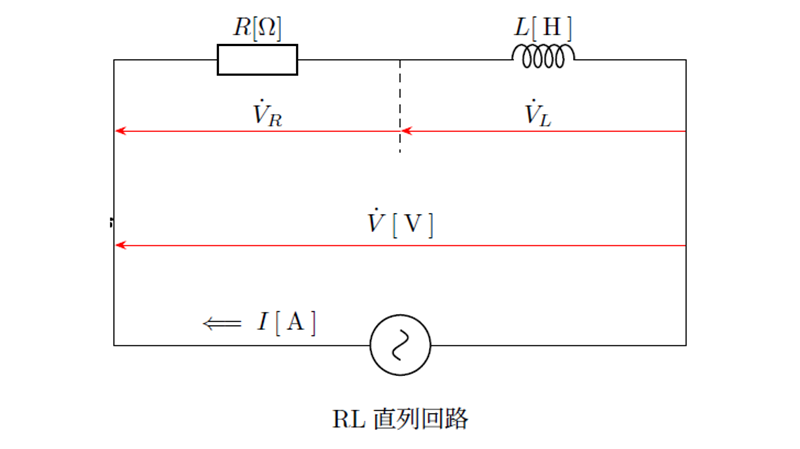
交流回路の直列接続
カテゴリー
-
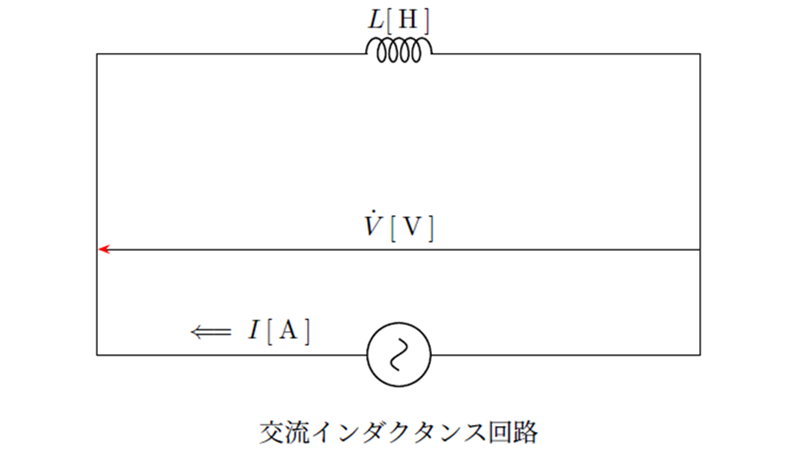
交流回路
カテゴリー
テスト投稿
-

2025年1月NISA運用概況
続きを読む
-

2025年1月金運用概況
続きを読む
-

可変抵抗器の直列回路
続きを読む
-

Packet Tracer
続きを読む
-

交流回路の直列接続
続きを読む
-

交流回路
続きを読む